最近公共祖先
描述
问题就是寻找树上两个节点的最近公共祖先节点
此题难度超过2500
现有一棵由 n 个节点组成的无向树,节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。
另给你一个长度为 m 的二维整数数组 queries ,其中 queries[i] = [ai, bi] 。对于每条查询,请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中,你可以选择树上的任意一条边,并将其权重更改为任意值。
注意:
- 查询之间 相互独立 的,这意味着每条新的查询时,树都会回到 初始状态 。
- 从
ai 到 bi的路径是一个由 不同 节点组成的序列,从节点 ai 开始,到节点 bi 结束,且序列中相邻的两个节点在树中共享一条边。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是第 i 条查询的答案。
示例 1:
1
2
3
4
5
6
7
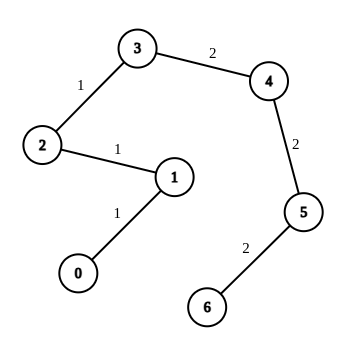
| 输入:n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出:[0,0,1,3]
解释:第 1 条查询,从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此,答案为 0 。
第 2 条查询,从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 0 。
第 3 条查询,将边 [2,3] 的权重变更为 2 。在这次操作之后,从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 1 。
第 4 条查询,将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后,从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
|
示例 2:
1
2
3
4
5
6
7
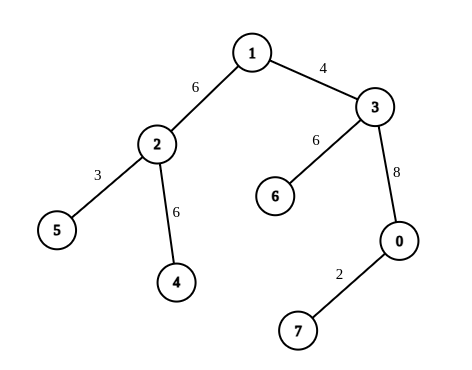
| 输入:n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出:[1,2,2,3]
解释:第 1 条查询,将边 [1,3] 的权重变更为 6 。在这次操作之后,从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此,答案为 1 。
第 2 条查询,将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后,从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 3 条查询,将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后,从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此,答案为 2 。
第 4 条查询,将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后,从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此,答案为 3 。
对于每条查询 queries[i] ,可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。
|
提示:
1 <= n <= 10^4edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 26- 生成的输入满足
edges 表示一棵有效的树
1 <= queries.length == m <= 2 * 10^4queries[i].length == 20 <= ai, bi < n
计算每个点的路径权重统计信息 + 树上倍增获得公共祖先
树上倍增获得公共祖先参考了灵神的题解
通过计算从0到每个点的路径权重统计信息 cnt
具体来说,比如x和y两个点,分别计算从0到x和y的路径权重统计,再减去从0到x和y的lca节点的路径权重统计的两倍(因为从0到lca节点的路径被x和y分别计算了一次),得到x和y之间的路径的权重
这种计算cnt的方法比较简单,但是不通用,比如把问题改成维护路径上的边权最大值,这种做法就不行了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
| class Solution {
public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {
int root = 0, cnt[][] = new int[n][0], depth[] = new int[n];
cnt[0] = new int[26];
int m = 32 - Integer.numberOfLeadingZeros(n), pa[][] = new int[n][m];
for (int t[] : pa) Arrays.fill(t, -1);
List<int[]> g[] = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int edge[] : edges) {
int u = edge[0], v = edge[1], w = edge[2]-1;
g[u].add(new int[]{v, w});
g[v].add(new int[]{u, w});
}
dfs(-1, 0, g, pa, cnt, depth);
for (int i = 0; i < m-1; i++) {
for (int x = 0; x < n; x++) {
int p = pa[x][i];
if (p == -1) continue;
int pp = pa[p][i];
pa[x][i+1] = pp;
}
}
int res[] = new int[queries.length];
for (int qi = 0; qi < queries.length; qi++) {
int query[] = queries[qi], x = query[0], y = query[1];
int pathLen = depth[x] + depth[y];
int cw[] = new int[26];
for (int i = 0; i < 26; i++) {
cw[i] += cnt[x][i];
cw[i] += cnt[y][i];
}
if (depth[x] > depth[y]) {
int t = x;
x = y;
y = t;
}
for (int k = depth[y] - depth[x]; k > 0; k &= k-1) {
int i = Integer.numberOfTrailingZeros(k);
int p = pa[y][i];
y = p;
}
if (y != x) {
for (int i = m-1; i >= 0; i--) {
int px = pa[x][i], py = pa[y][i];
if (px != py) {
x = px;
y = py;
}
}
x = pa[x][0];
}
int lca = x;
pathLen -= depth[lca]*2;
int maxCw = 0;
for (int i = 0; i < 26; i++) {
cw[i] -= cnt[lca][i]*2;
}
for (int i = 0; i < 26; i++) maxCw = Math.max(maxCw, cw[i]);
res[qi] = pathLen - maxCw;
}
return res;
}
public void dfs(int pre, int cur, List<int[]> g[], int pa[][], int cnt[][], int depth[]) {
pa[cur][0] = pre;
for (int nxt[] : g[cur]) {
int v = nxt[0], w = nxt[1];
if (v == pre) continue;
cnt[v] = cnt[cur].clone();
cnt[v][w]++;
depth[v] = depth[cur] + 1;
dfs(cur, v, g, pa, cnt, depth);
}
}
}
|
cnt 和 pa数组一样使用 树上倍增 的方式计算
这个做法才是灵神推荐和采取的做法,虽然写起来更难,但是通用性更高,这里的cnt可以适用于解决其它类似问题,比如灵神说的维护路径上的边权最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| class Solution {
public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {
int m = 32 - Integer.numberOfLeadingZeros(n), depth[] = new int[n];
int cnt[][][] = new int[n][m][26], pa[][] = new int[n][m];
for (int t[] : pa) Arrays.fill(t, -1);
List<int[]> g[] = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int edge[] : edges) {
int u = edge[0], v = edge[1], w = edge[2]-1;
g[u].add(new int[]{v, w});
g[v].add(new int[]{u, w});
}
dfs(-1, 0, g, pa, cnt, depth);
for (int i = 0; i < m-1; i++) {
for (int x = 0; x < n; x++) {
int p = pa[x][i];
if (p == -1) continue;
int pp = pa[p][i];
pa[x][i+1] = pp;
for (int j = 0; j < 26; j++) {
cnt[x][i+1][j] = cnt[x][i][j] + cnt[p][i][j];
}
}
}
int res[] = new int[queries.length];
for (int qi = 0; qi < queries.length; qi++) {
int query[] = queries[qi], x = query[0], y = query[1];
int pathLen = depth[x] + depth[y];
int cw[] = new int[26];
if (depth[x] > depth[y]) {
int t = x;
x = y;
y = t;
}
for (int k = depth[y] - depth[x]; k > 0; k &= k-1) {
int i = Integer.numberOfTrailingZeros(k);
int p = pa[y][i];
for (int j = 0; j < 26; j++) {
cw[j] += cnt[y][i][j];
}
y = p;
}
if (y != x) {
for (int i = m-1; i >= 0; i--) {
int px = pa[x][i], py = pa[y][i];
if (px != py) {
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][i][j] + cnt[y][i][j];
}
x = px;
y = py;
}
}
for (int j = 0; j < 26; j++) {
cw[j] += cnt[x][0][j] + cnt[y][0][j];
}
x = pa[x][0];
}
int lca = x;
pathLen -= depth[lca]*2;
int maxCw = 0;
for (int i = 0; i < 26; i++) maxCw = Math.max(maxCw, cw[i]);
res[qi] = pathLen - maxCw;
}
return res;
}
public void dfs(int pre, int cur, List<int[]> g[], int pa[][], int cnt[][][], int depth[]) {
pa[cur][0] = pre;
for (int nxt[] : g[cur]) {
int v = nxt[0], w = nxt[1];
if (v == pre) continue;
cnt[v][0][w] = 1;
depth[v] = depth[cur] + 1;
dfs(cur, v, g, pa, cnt, depth);
}
}
}
|


