KMP算法概念
KMP算法是一种用于字符串匹配的经典算法,它的全名是Knuth-Morris-Pratt算法,是由Donald Knuth、Vaughan Pratt和James H. Morris分别独立发明的。KMP算法用于在一个主文本字符串中查找一个模式字符串的出现,它的主要优势在于在匹配失败时避免不必要的回溯。
KMP算法通过构建部分匹配表(Partial Match Table),也称为最长前缀后缀匹配表(Longest Prefix Suffix Table),来避免这种不必要的比较。
性能分析
KMP算法的时间复杂度为O(m + n),其中m是主文本字符串的长度,n是模式字符串的长度。
参考
算法学习笔记(13): KMP算法
模板
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 public static int [] getPmt(char [] pattern) { int pmt[] = new int [pattern.length]; for (int i = 1 , j = 0 ; i < pattern.length; i++) { while (j != 0 && pattern[i] != pattern[j]) j = pmt[j - 1 ]; if (pattern[i] == pattern[j]) j++; pmt[i] = j; } return pmt; } public static int count (char [] s, char [] p, int [] pmt) { int res = 0 ; for (int i = 0 , j = 0 ; i < s.length; i++) { while (j != 0 && s[i] != p[j]) j = pmt[j - 1 ]; if (s[i] == p[j]) j++; if (j == p.length) { res += 1 ; j = pmt[j - 1 ]; } } return res; }
题目描述
给出两个字符串 s 1 s_1 s 1 s 2 s_2 s 2 s 1 s_1 s 1 [ l , r ] [l, r] [ l , r ] s 2 s_2 s 2 s 2 s_2 s 2 s 1 s_1 s 1 l l l s 2 s_2 s 2 s 1 s_1 s 1
定义一个字符串 s s s s s s 非 s s s 的子串 t t t t t t s s s s s s s 2 s_2 s 2 s ′ s' s ′ t ′ t' t ′
输入格式
第一行为一个字符串,即为 s 1 s_1 s 1 s 2 s_2 s 2
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序 输出 s 2 s_2 s 2 s 1 s_1 s 1 ∣ s 2 ∣ |s_2| ∣ s 2 ∣ i i i s 2 s_2 s 2 i i i
样例 #1
样例输入 #1
样例输出 #1
提示
样例 1 解释
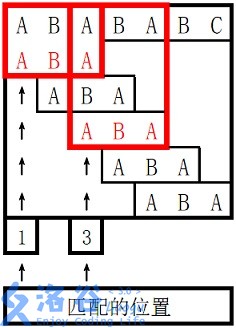
对于 s 2 s_2 s 2 3 3 3 ABA,字符串 A 既是其后缀也是其前缀,且是最长的,因此最长 border 长度为 1 1 1
数据规模与约定
本题采用多测试点捆绑测试,共有 3 个子任务 。
Subtask 1(30 points):∣ s 1 ∣ ≤ 15 |s_1| \leq 15 ∣ s 1 ∣ ≤ 15 ∣ s 2 ∣ ≤ 5 |s_2| \leq 5 ∣ s 2 ∣ ≤ 5
Subtask 2(40 points):∣ s 1 ∣ ≤ 1 0 4 |s_1| \leq 10^4 ∣ s 1 ∣ ≤ 1 0 4 ∣ s 2 ∣ ≤ 1 0 2 |s_2| \leq 10^2 ∣ s 2 ∣ ≤ 1 0 2
Subtask 3(30 points):无特殊约定。
对于全部的测试点,保证 1 ≤ ∣ s 1 ∣ , ∣ s 2 ∣ ≤ 1 0 6 1 \leq |s_1|,|s_2| \leq 10^6 1 ≤ ∣ s 1 ∣ , ∣ s 2 ∣ ≤ 1 0 6 s 1 , s 2 s_1, s_2 s 1 , s 2
KMP算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 import java.util.Scanner;public class Main { public static int [] getPmt(char [] pattern) { int pmt[] = new int [pattern.length]; for (int i = 1 , j = 0 ; i < pattern.length; i++) { while (j != 0 && pattern[i] != pattern[j]) j = pmt[j - 1 ]; if (pattern[i] == pattern[j]) j++; pmt[i] = j; } return pmt; } public static int count (char [] s, char [] p, int [] pmt) { int res = 0 ; for (int i = 0 , j = 0 ; i < s.length; i++) { while (j != 0 && s[i] != p[j]) j = pmt[j - 1 ]; if (s[i] == p[j]) j++; if (j == p.length) { res += 1 ; System.out.println(i - j + 2 ); j = pmt[j - 1 ]; } } return res; } public static void main (String[] args) { Scanner in = new Scanner (System.in); while (in.hasNext()) { char s[] = in.next().toCharArray(), p[] = in.next().toCharArray(); int [] pmt = getPmt(p); count(s, p, pmt); for (int i = 0 ; i < p.length; i++) { System.out.print(pmt[i] + " " ); } } } }
3529. 统计水平子串和垂直子串重叠格子的数目
给你一个由字符组成的 m x n 矩阵 grid 和一个字符串 pattern。
水平子串 是从左到右的一段连续字符序列。如果子串到达了某行的末尾,它将换行并从下一行的第一个字符继续。不会 从最后一行回到第一行。
垂直子串 是从上到下的一段连续字符序列。如果子串到达了某列的底部,它将换列并从下一列的第一个字符继续。不会 从最后一列回到第一列。
请统计矩阵中满足以下条件的单元格数量:
该单元格必须属于 至少 一个等于 pattern 的水平子串,且属于 至少 一个等于 pattern 的垂直子串。
返回满足条件的单元格数量。
示例 1:
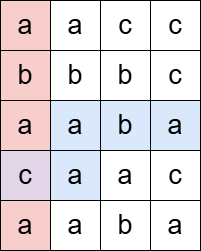
输入: grid = [[“a”,“a”,“c”,“c”],[“b”,“b”,“b”,“c”],[“a”,“a”,“b”,“a”],[“c”,“a”,“a”,“c”],[“a”,“a”,“b”,“a”]], pattern = “abaca”
输出: 1
解释:
"abaca" 作为一个水平子串(蓝色)和一个垂直子串(红色)各出现一次,并在一个单元格(紫色)处相交。
示例 2:
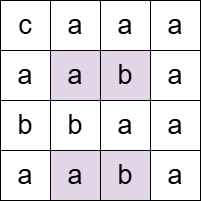
输入: grid = [[“c”,“a”,“a”,“a”],[“a”,“a”,“b”,“a”],[“b”,“b”,“a”,“a”],[“a”,“a”,“b”,“a”]], pattern = “aba”
输出: 4
解释:
上述被标记的单元格都同时属于至少一个 "aba" 的水平和垂直子串。
示例 3:
输入: grid = [[“a”]], pattern = “a”
输出: 1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 10^51 <= pattern.length <= m * ngrid 和 pattern 仅由小写英文字母组成。
kmp + 手动计算覆盖
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 class Solution { public static int [] getPmt(char [] pattern) { int pmt[] = new int [pattern.length]; for (int i = 1 , j = 0 ; i < pattern.length; i++) { while (j != 0 && pattern[i] != pattern[j]) j = pmt[j - 1 ]; if (pattern[i] == pattern[j]) j++; pmt[i] = j; } return pmt; } public static int [] count(char [] s, char [] p, int [] pmt) { int [] res = new int [s.length]; for (int i = 0 , j = 0 ; i < s.length; i++) { while (j != 0 && s[i] != p[j]) j = pmt[j - 1 ]; if (s[i] == p[j]) j++; if (j == p.length) { res[i-j+1 ] = 1 ; j = pmt[j - 1 ]; } } return res; } public int countCells (char [][] grid, String pattern) { StringBuilder sb1 = new StringBuilder (), sb2 = new StringBuilder (); int m = grid.length, n = grid[0 ].length; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sb1.append(grid[i][j]); } } for (int j = 0 ; j < n; j++) { for (int i = 0 ; i < m; i++) { sb2.append(grid[i][j]); } } String s1 = sb1.toString(), s2 = sb2.toString(); char [] p = pattern.toCharArray(), cs1 = s1.toCharArray(), cs2 = s2.toCharArray(); int [] cnt1 = count(cs1, p, getPmt(p)), cnt2 = count(cs2, p, getPmt(p)); put(cnt1, p.length); put(cnt2, p.length); int res = 0 ; for (int idx1 = 0 ; idx1 < cnt1.length; idx1++) { int i = idx1/n, j = idx1%n; int idx2 = j*m+i; if (cnt1[idx1] == 1 && cnt2[idx2] == 1 ) res++; } return res; } public void put (int [] cnt, int pLen) { int pre = -1 ; for (int i = 0 ; i < cnt.length; i++) { if (cnt[i] == 1 ) pre = i; if (pre == -1 ) continue ; if (i - pre < pLen) cnt[i] = 1 ; } } }
kmp + 差分
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 class Solution { public static int [] getPmt(char [] pattern) { int pmt[] = new int [pattern.length]; for (int i = 1 , j = 0 ; i < pattern.length; i++) { while (j != 0 && pattern[i] != pattern[j]) j = pmt[j - 1 ]; if (pattern[i] == pattern[j]) j++; pmt[i] = j; } return pmt; } public static int [] count(char [] s, char [] p, int [] pmt) { int [] res = new int [s.length+1 ]; for (int i = 0 , j = 0 ; i < s.length; i++) { while (j != 0 && s[i] != p[j]) j = pmt[j - 1 ]; if (s[i] == p[j]) j++; if (j == p.length) { res[i-j+1 ]++; res[i+1 ]--; j = pmt[j - 1 ]; } } for (int i = 0 ; i < s.length; i++) { res[i+1 ] += res[i]; } return res; } public int countCells (char [][] grid, String pattern) { StringBuilder sb1 = new StringBuilder (), sb2 = new StringBuilder (); int m = grid.length, n = grid[0 ].length; for (int i = 0 ; i < m; i++) { for (int j = 0 ; j < n; j++) { sb1.append(grid[i][j]); } } for (int j = 0 ; j < n; j++) { for (int i = 0 ; i < m; i++) { sb2.append(grid[i][j]); } } String s1 = sb1.toString(), s2 = sb2.toString(); char [] p = pattern.toCharArray(), cs1 = s1.toCharArray(), cs2 = s2.toCharArray(); int [] cnt1 = count(cs1, p, getPmt(p)), cnt2 = count(cs2, p, getPmt(p)); int res = 0 ; for (int idx1 = 0 ; idx1 < cnt1.length; idx1++) { int i = idx1/n, j = idx1%n; int idx2 = j*m+i; if (cnt1[idx1] > 0 && cnt2[idx2] > 0 ) res++; } return res; } }
 。
。