834. 树中距离之和

给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。

给定整数 n 和数组 edges ， edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。

返回长度为 n 的数组 answer ，其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。

示例 1:

1
2
3
4
5
输入: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

示例 2:

1
2
输入: n = 1, edges = []
输出: [0]

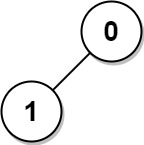
示例 3:

1
2
输入: n = 2, edges = [[1,0]]
输出: [1,1]

提示:

  • 1 <= n <= 3 * 10^4
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • 给定的输入保证为有效的树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    int res[], size[];
    public int[] sumOfDistancesInTree(int n, int[][] edges) {
        res = new int[n];  // 保存结果
        size = new int[n];  // 保存每个子树的大小
        List<Integer> g[] = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int[] edge : edges) {
            g[edge[0]].add(edge[1]);
            g[edge[1]].add(edge[0]);
        }
        dfs(0, 0, 0, g);  // 计算0节点为root的结果
        reroot(0, 0, g);  // 通过换根计算以其它节点为root的结果
        return res;
    }
    public void dfs(int pre, int cur, int depth, List<Integer> g[]) {
        res[0] += depth;
        size[cur] = 1;
        for (int next : g[cur]) {
            if (next == pre) continue;
            dfs(cur, next, depth+1, g);
            size[cur] += size[next];
        }
    }
    public void reroot(int pre, int cur, List<Integer> g[]) {
        for (int next : g[cur]) {
            if (next == pre) continue;
            // 换根：res[next] = res[cur] - size[next] + (n-size[next]);
            res[next] = res[cur] + res.length - 2 * size[next];
            reroot(cur, next, g);
        }
    }
}