3123. 最短路径中的边
给你一个 n 个节点的无向带权图,节点编号为 0 到 n - 1 。图中总共有 m 条边,用二维数组 edges 表示,其中 edges[i] = [ai, bi, wi] 表示节点 ai 和 bi 之间有一条边权为 wi 的边。
对于节点 0 为出发点,节点 n - 1 为结束点的所有最短路,你需要返回一个长度为 m 的 boolean 数组 answer ,如果 edges[i] 至少 在其中一条最短路上,那么 answer[i] 为 true ,否则 answer[i] 为 false 。
请你返回数组 answer 。
注意,图可能不连通。
示例 1:
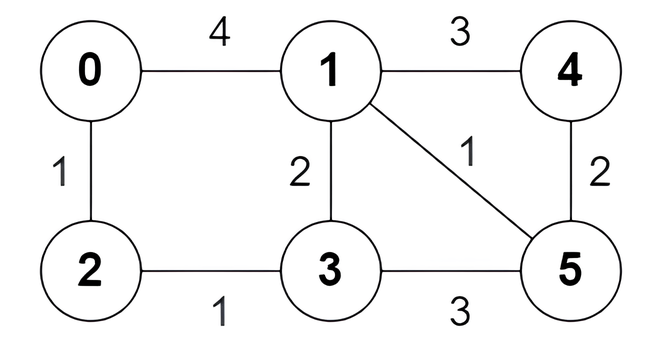
**输入:**n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]
输出:[true,true,true,false,true,true,true,false]
解释:
以下为节点 0 出发到达节点 5 的 所有 最短路:
- 路径
0 -> 1 -> 5 :边权和为 4 + 1 = 5 。
- 路径
0 -> 2 -> 3 -> 5 :边权和为 1 + 1 + 3 = 5 。
- 路径
0 -> 2 -> 3 -> 1 -> 5 :边权和为 1 + 1 + 2 + 1 = 5 。
示例 2:
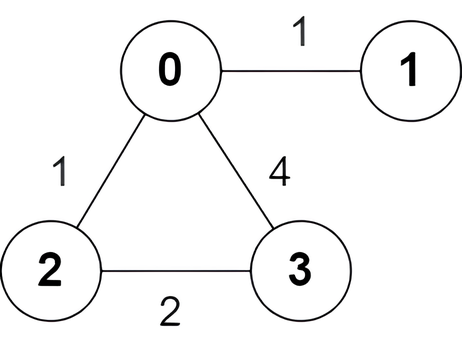
**输入:**n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]
输出:[true,false,false,true]
解释:
只有一条从节点 0 出发到达节点 3 的最短路 0 -> 2 -> 3 ,边权和为 1 + 2 = 3 。
提示:
2 <= n <= 5 * 10^4m == edges.length1 <= m <= min(5 * 10^4, n * (n - 1) / 2)0 <= ai, bi < nai != bi1 <= wi <= 10^5- 图中没有重边。
记录父节点进行回溯的Dijkstra
题目需要求解哪些边是在最短路径上的,所以在求最短路的同时,我们需要记录当前最短路节点的父节点,在求得最短路径后(可能不止一条),我们通过每个节点的父节点进行回溯,即可找到最短路上的边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
| class Solution {
public boolean[] findAnswer(int n, int[][] edges) {
List<int[]> g[] = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < edges.length; i++) {
int edge[] = edges[i];
int x = edge[0], y = edge[1], w = edge[2];
g[x].add(new int[]{y, w});
g[y].add(new int[]{x, w});
map.put(x*n+y, i);
map.put(y*n+x, i);
}
int dis[] = new int[n];
Arrays.fill(dis, Integer.MAX_VALUE);
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);
dis[0] = 0;
pq.offer(new int[]{0, 0});
Set<Integer> p[] = new HashSet[n];
Arrays.setAll(p, i -> new HashSet<>());
while (!pq.isEmpty()) {
int poll[] = pq.poll(), cur = poll[0], curDis = poll[1];
for (int nxt[] : g[cur]) {
int y = nxt[0], w = nxt[1];
if (curDis + w <= dis[y]) {
if (curDis + w < dis[y]) {
p[y] = new HashSet<>();
}
p[y].add(cur);
dis[y] = curDis + w;
pq.offer(new int[]{y, dis[y]});
}
}
}
Deque<Integer> dq = new ArrayDeque<>();
dq.offer(n-1);
boolean res[] = new boolean[edges.length];
while (!dq.isEmpty()) {
int poll = dq.poll();
for (int pa : p[poll]) {
if (res[map.get(pa*n+poll)] == true) continue;
res[map.get(pa*n+poll)] = true;
dq.offer(pa);
}
}
return res;
}
}
|
双边Dijkstra
正向dijkstra获得节点0到节点n-1的最短路径:dis[]
反向dijkstra获得节点n-1到节点0的最短路径:dis2[]
判断每一条边是否在最短路径上,比如一条边:(u,v,w),我们可以通过判断 dis[x] + dis2[y] + w == dis[n-1] || dis[y] + dis2[x] + w == dis[n-1] 来判断这一条边是否在最短路上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| class Solution {
public boolean[] findAnswer(int n, int[][] edges) {
List<int[]> g[] = new ArrayList[n];
Arrays.setAll(g, i -> new ArrayList<>());
for (int i = 0; i < edges.length; i++) {
int edge[] = edges[i];
int x = edge[0], y = edge[1], w = edge[2];
g[x].add(new int[]{y, w});
g[y].add(new int[]{x, w});
}
int dis[] = new int[n];
Arrays.fill(dis, Integer.MAX_VALUE);
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);
dis[0] = 0;
pq.offer(new int[]{0, 0});
while (!pq.isEmpty()) {
int poll[] = pq.poll(), cur = poll[0], d = poll[1];
for (int nxt[] : g[cur]) {
int y = nxt[0], w = nxt[1];
if (d + w < dis[y]) {
dis[y] = d + w;
pq.offer(new int[]{y, dis[y]});
}
}
}
int dis2[] = new int[n];
Arrays.fill(dis2, Integer.MAX_VALUE);
dis2[n-1] = 0;
pq.offer(new int[]{n-1, 0});
while (!pq.isEmpty()) {
int poll[] = pq.poll(), cur = poll[0], d = poll[1];
for (int nxt[] : g[cur]) {
int y = nxt[0], w = nxt[1];
if (d + w < dis2[y]) {
dis2[y] = d + w;
pq.offer(new int[]{y, dis2[y]});
}
}
}
boolean res[] = new boolean[edges.length];
for (int i = 0; i < edges.length; i++) {
int e[] = edges[i], x = e[0], y = e[1], w = e[2];
if (dis[x] + dis2[y] + w == dis[n-1] || dis[y] + dis2[x] + w == dis[n-1]) res[i] = true;
}
return res;
}
}
|


