2920. 收集所有金币可获得的最大积分 (2351)
节点 0 处现有一棵由 n 个节点组成的无向树,节点编号从 0 到 n - 1 。给你一个长度为 n - 1 的二维 整数 数组 edges ,其中 edges[i] = [ai, bi] 表示在树上的节点 ai 和 bi 之间存在一条边。另给你一个下标从 0 开始、长度为 n 的数组 coins 和一个整数 k ,其中 coins[i] 表示节点 i 处的金币数量。
从根节点开始,你必须收集所有金币。要想收集节点上的金币,必须先收集该节点的祖先节点上的金币。
节点 i 上的金币可以用下述方法之一进行收集:
收集所有金币,得到共计 coins[i] - k 点积分。如果 coins[i] - k 是负数,你将会失去 abs(coins[i] - k) 点积分。
收集所有金币,得到共计 floor(coins[i] / 2) 点积分。如果采用这种方法,节点 i 子树中所有节点 j 的金币数 coins[j] 将会减少至 floor(coins[j] / 2) 。
返回收集 所有 树节点的金币之后可以获得的最大积分。
示例 1:
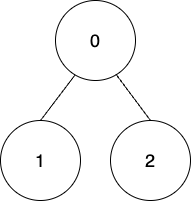
1 2 3 4 5 6 7 8 输入:edges = [[0,1],[1,2],[2,3]], coins = [10,10,3,3], k = 5 输出:11 解释: 使用第一种方法收集节点 0 上的所有金币。总积分 = 10 - 5 = 5 。 使用第一种方法收集节点 1 上的所有金币。总积分 = 5 + (10 - 5) = 10 。 使用第二种方法收集节点 2 上的所有金币。所以节点 3 上的金币将会变为 floor(3 / 2) = 1 ,总积分 = 10 + floor(3 / 2) = 11 。 使用第二种方法收集节点 3 上的所有金币。总积分 = 11 + floor(1 / 2) = 11. 可以证明收集所有节点上的金币能获得的最大积分是 11 。
示例 2:
1 2 3 4 输入:edges = [[0,1],[0,2]], coins = [8,4,4], k = 0 输出:16 解释: 使用第一种方法收集所有节点上的金币,因此,总积分 = (8 - 0) + (4 - 0) + (4 - 0) = 16 。
提示:
n == coins.length2 <= n <= 10^50 <= coins[i] <= 10^4edges.length == n - 10 <= edges[i][0], edges[i][1] < n0 <= k <= 10^4
树形dp,用记忆化搜索实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { int cache[][]; public int maximumPoints (int [][] edges, int [] coins, int k) { int n = coins.length; List<Integer> g[] = new ArrayList [n]; Arrays.setAll(g, i -> new ArrayList <>()); for (int e[] : edges) { g[e[0 ]].add(e[1 ]); g[e[1 ]].add(e[0 ]); } cache = new int [n][15 ]; for (int c[] : cache) Arrays.fill(c, -1 ); return dfs(0 , -1 , 0 , coins, g, k); } int dfs (int u, int p, int times, int coins[], List<Integer> g[], int k) { if (cache[u][times] != -1 ) return cache[u][times]; int res[] = new int [2 ], value = coins[u] >> times; res[0 ] = value - k; res[1 ] = value / 2 ; int nextTimes = Math.min(times+1 , 14 ); for (int v : g[u]) { if (v != p) { res[0 ] += dfs(v, u, times, coins, g, k); res[1 ] += dfs(v, u, nextTimes, coins, g, k); } } cache[u][times] = Math.max(res[0 ], res[1 ]); return cache[u][times]; } }