2812. 找出最安全路径(2154)
给你一个下标从 0 开始、大小为 n x n 的二维矩阵 grid ,其中 (r, c) 表示:
- 如果
grid[r][c] = 1 ,则表示一个存在小偷的单元格
- 如果
grid[r][c] = 0 ,则表示一个空单元格
你最开始位于单元格 (0, 0) 。在一步移动中,你可以移动到矩阵中的任一相邻单元格,包括存在小偷的单元格。
矩阵中路径的 安全系数 定义为:从路径中任一单元格到矩阵中任一小偷所在单元格的 最小 曼哈顿距离。
返回所有通向单元格 (n - 1, n - 1) 的路径中的 最大安全系数 。
单元格 (r, c) 的某个 相邻 单元格,是指在矩阵中存在的 (r, c + 1)、(r, c - 1)、(r + 1, c) 和 (r - 1, c) 之一。
两个单元格 (a, b) 和 (x, y) 之间的 曼哈顿距离 等于 | a - x | + | b - y | ,其中 |val| 表示 val 的绝对值。
示例 1:
1
2
3
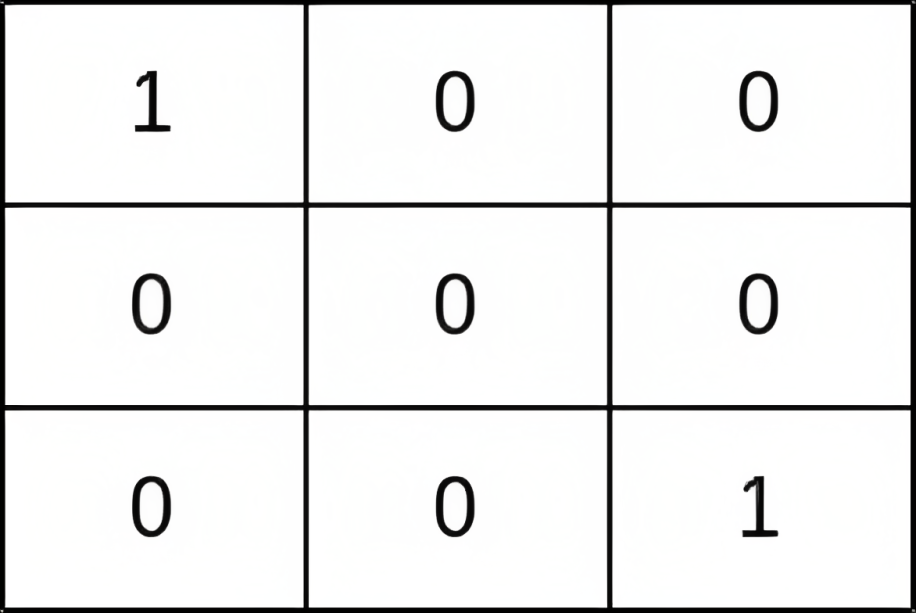
| 输入:grid = [[1,0,0],[0,0,0],[0,0,1]]
输出:0
解释:从 (0, 0) 到 (n - 1, n - 1) 的每条路径都经过存在小偷的单元格 (0, 0) 和 (n - 1, n - 1) 。
|
示例 2:
1
2
3
4
5
6
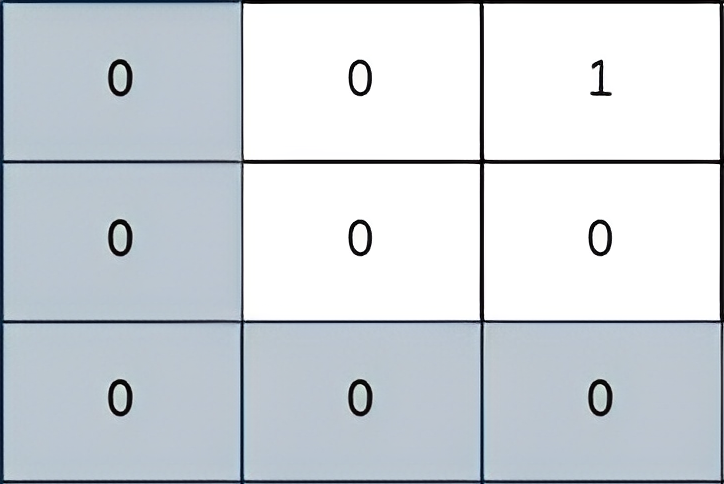
| 输入:grid = [[0,0,1],[0,0,0],[0,0,0]]
输出:2
解释:
上图所示路径的安全系数为 2:
- 该路径上距离小偷所在单元格(0,2)最近的单元格是(0,0)。它们之间的曼哈顿距离为 | 0 - 0 | + | 0 - 2 | = 2 。
可以证明,不存在安全系数更高的其他路径。
|
示例 3:
1
2
3
4
5
6
7
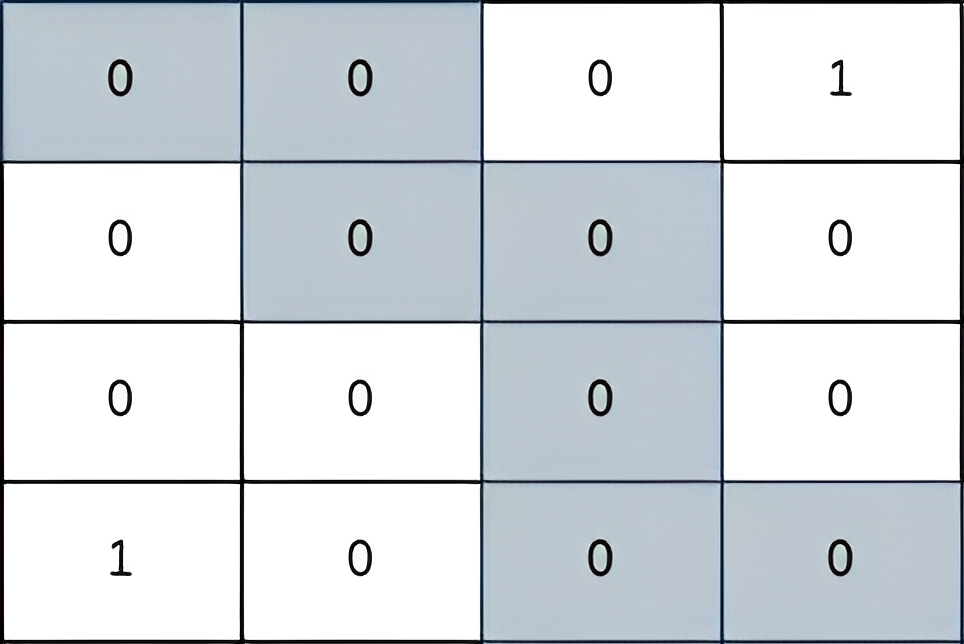
| 输入:grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
输出:2
解释:
上图所示路径的安全系数为 2:
- 该路径上距离小偷所在单元格(0,3)最近的单元格是(1,2)。它们之间的曼哈顿距离为 | 0 - 1 | + | 3 - 2 | = 2 。
- 该路径上距离小偷所在单元格(3,0)最近的单元格是(3,2)。它们之间的曼哈顿距离为 | 3 - 3 | + | 0 - 2 | = 2 。
可以证明,不存在安全系数更高的其他路径。
|
提示:
1 <= grid.length == n <= 400grid[i].length == ngrid[i][j] 为 0 或 1grid 至少存在一个小偷
bfs + dijkstra构造路径
用bfs算出所有点的安全系数security,用数组dis保存
找到所有值为1的点,同时往外层bfs扩散
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public int maximumSafenessFactor(List<List<Integer>> grid) {
int n = grid.size();
int dis[][] = new int[n][n];
for (int[] arr : dis) Arrays.fill(arr, -1);
Queue<int[]> q = new LinkedList<>();
for (int i = 0; i < n; i++) {
List<Integer> l = grid.get(i);
for (int j = 0; j < n; j++) {
if (l.get(j) == 1) {
dis[i][j] = 0;
q.add(new int[]{i, j});
}
}
}
int dir[] = new int[]{0, 1, 0, -1, 0};
int curDis = 1;
while (!q.isEmpty()) {
int sz = q.size();
for (int t = 0; t < sz; t++) {
int[] poll = q.poll();
int x = poll[0], y = poll[1];
for (int i = 0; i < dir.length - 1; i++) {
int nx = x + dir[i], ny = y + dir[i + 1];
if (nx < 0 || ny < 0 || nx > n-1 || ny > n-1 || dis[nx][ny] >= 0) continue;
dis[nx][ny] = curDis;
q.offer(new int[]{nx, ny});
}
}
curDis++;
}
return dij(0, 0, dis);
}
|
接着,用dijkstra算法实现dij函数,每次优先考虑安全系数最高的点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| private int dij(int sx, int sy, int[][] dis) {
int n = dis.length;
int[][] minSecurity = new int[n][n];
for (int[] arr : minSecurity) Arrays.fill(arr, -1);
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> b[0] - a[0]);
minSecurity[sx][sy] = dis[sx][sy];
pq.offer(new int[]{minSecurity[sx][sy], sx, sy});
while (!pq.isEmpty()) {
int[] poll = pq.poll();
int security = poll[0], x = poll[1], y = poll[2];
int dir[] = new int[]{0, 1, 0, -1, 0};
for (int i = 0; i < dir.length - 1; i++) {
int nx = x + dir[i], ny = y + dir[i + 1];
if (nx < 0 || ny < 0 || nx > n - 1 || ny > n - 1) continue;
if (minSecurity[nx][ny] == -1 || (dis[nx][ny] >= security && security > minSecurity[nx][ny])) {
minSecurity[nx][ny] = Math.min(dis[nx][ny], security);
pq.offer(new int[]{minSecurity[nx][ny], nx, ny});
}
}
}
return minSecurity[n - 1][n - 1];
}
}
|
并查集构造路径解法 and 限制路径二分解法



