2322. 从树中删除边的最小分数

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点， 以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

  1. 分别获取三个组件 每个 组件中所有节点值的异或值。
  2. 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。
  • 例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = ***6***、1 ^ 9 = ***8*** 和 3 ^ 3 ^ 3 = ***3*** 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的 最小 分数。

示例 1：

1
2
3
4
5
6
7
8
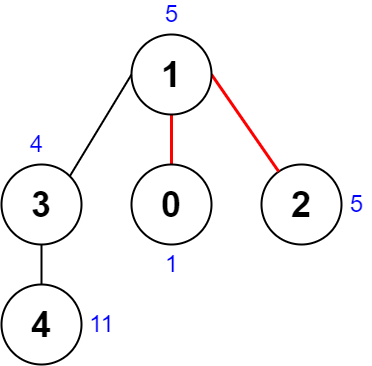
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

1
2
3
4
5
6
7
8
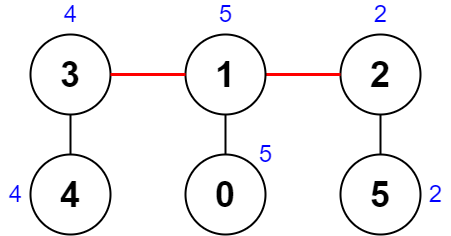
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

提示：

  • n == nums.length
  • 3 <= n <= 1000
  • 1 <= nums[i] <= 10^8
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵有效的树

dfs计算异或值 + dfs时间戳，判断两个节点的祖父关系

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
    int time;
    int[] xor, in, out;
    public int minimumScore(int[] nums, int[][] edges) {
        int n = nums.length;
        xor = new int[n];
        in = new int[n];
        out = new int[n];
        List<Integer> g[] = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int e[] : edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
        }
        dfs(-1, 0, g, nums);
        int res = (int)1e9;
        for (int i = 1, x, y, z; i < n; i++) {
            for (int j = i+1; j < n; j++) {
                if (in[i] < in[j] && in[j] <= out[i]) {  // i是j的祖先
                    x = xor[j];
                    y = xor[i] ^ xor[j];
                    z = xor[0] ^ xor[i];
                }
                else if (in[j] < in[i] && in[i] <= out[j]) {  // j是i的祖先
                    x = xor[i];
                    y = xor[j] ^ xor[i];
                    z = xor[0] ^ xor[j];
                }
                else {  // i和j在两颗子树上
                    x = xor[i];
                    y = xor[j];
                    z = xor[0] ^ xor[i] ^ xor[j];
                }
                int cur = Math.max(Math.max(x, y), z) - Math.min(Math.min(x, y), z);
                res = Math.min(res, cur);
            }
        }
        return res;
    }
    int dfs(int pre, int cur, List<Integer> g[], int nums[]) {
        in[cur] = ++time;  // 写成time++调试半天，晕
        int res = nums[cur];
        for (int nxt : g[cur]) {
            if (nxt == pre) continue;
            res ^= dfs(cur, nxt, g, nums);;
        }
        out[cur] = time;
        return xor[cur] = res;
    }
}

dfs也可以不用返回值

1
2
3
4
5
6
7
8
9
10
11

void dfs(int pre, int cur, List<Integer> g[], int nums[]) {
    in[cur] = ++time;  // 写成time++调试半天，晕
    xor[cur] = nums[cur];
    for (int nxt : g[cur]) {
        if (nxt == pre) continue;
        dfs(cur, nxt, g, nums);;
        xor[cur] ^= xor[nxt];
    }
    out[cur] = time;
}