2127. 参加会议的最多员工数

一个公司准备组织一场会议，邀请名单上有 n 位员工。公司准备了一张 圆形 的桌子，可以坐下 任意数目 的员工。

员工编号为 0 到 n - 1 。每位员工都有一位 喜欢 的员工，每位员工 当且仅当 他被安排在喜欢员工的旁边，他才会参加会议。每位员工喜欢的员工 不会 是他自己。

给你一个下标从 0 开始的整数数组 favorite ，其中 favorite[i] 表示第 i 位员工喜欢的员工。请你返回参加会议的 最多员工数目 。

示例 1：

1
2
3
4
5
6
7
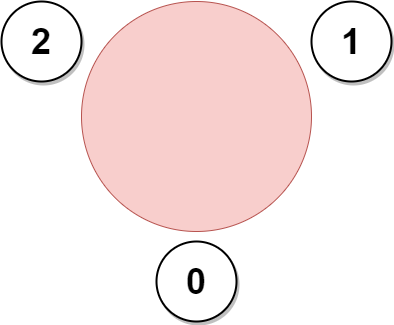
输入：favorite = [2,2,1,2]
输出：3
解释：
上图展示了公司邀请员工 0，1 和 2 参加会议以及他们在圆桌上的座位。
没办法邀请所有员工参与会议，因为员工 2 没办法同时坐在 0，1 和 3 员工的旁边。
注意，公司也可以邀请员工 1，2 和 3 参加会议。
所以最多参加会议的员工数目为 3 。

示例 2：

1
2
3
4
5
6
7
8
9
输入：favorite = [1,2,0]
输出：3
解释：
每个员工都至少是另一个员工喜欢的员工。所以公司邀请他们所有人参加会议的前提是所有人都参加了会议。
座位安排同图 1 所示：
- 员工 0 坐在员工 2 和 1 之间。
- 员工 1 坐在员工 0 和 2 之间。
- 员工 2 坐在员工 1 和 0 之间。
参与会议的最多员工数目为 3 。

示例 3：

1
2
3
4
5
6
7
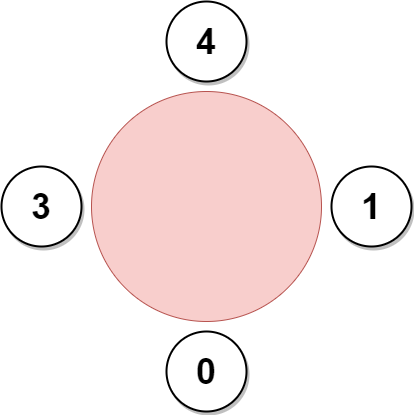
输入：favorite = [3,0,1,4,1]
输出：4
解释：
上图展示了公司可以邀请员工 0，1，3 和 4 参加会议以及他们在圆桌上的座位。
员工 2 无法参加，因为他喜欢的员工 1 旁边的座位已经被占领了。
所以公司只能不邀请员工 2 。
参加会议的最多员工数目为 4 。

提示：

  • n == favorite.length
  • 2 <= n <= 10^5
  • 0 <= favorite[i] <= n - 1
  • favorite[i] != i

拓扑排序

拓扑排序找环并记录链长度 + 环长度的分类讨论

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    public int maximumInvitations(int[] favorite) {
        int res = 0, n = favorite.length, len[] = new int[n], degree[] = new int[n];
        // 使用拓扑排序可以分割图中的链和环，拓扑排序删除入度为0的节点后，剩下的就是那些环
        for (int i = 0; i < n; i++) {
            degree[favorite[i]] += 1;
        }
        Deque<Integer> q = new ArrayDeque<>();
        for (int i = 0; i < n; i++) {
            if (degree[i] == 0) {
                q.offer(i);
            }
        }
        while (!q.isEmpty()) {
            int p = q.poll();
            int v = favorite[p];
            // len[v] = Math.max(len[v], len[p] + 1);
            // 拓扑排序的同时，计算当前链的长度
            len[v] = len[p] + 1;  // 因为是bfs遍历，所以len更长的情况肯定是在后面赋值（不会被更短的len值覆盖）
            if (--degree[v] == 0) {
                q.offer(v);
            }
        }
        // 如果环的长度大于等于3，那么由于环内的点相互制约，就只能是坐下这个环的人
        // 如果这个环的长度是2（可能有多个），那么它就是由两个点组成的环，这两个点只要相邻，空位可以放入其它相连的节点，最大化节点数量就是把两个点的链都放进来
        int chainSize = 0;  
        for (int i = 0; i < n; i++) {
            if (degree[i] == 0) continue;
            degree[i] = 0;
            int cnt = 1;
            for (int cur = favorite[i]; cur != i; cur = favorite[cur]) {
                cnt += 1;
                degree[cur] = 0;
            }
            if (cnt == 2) {
                chainSize += len[i] + len[favorite[i]] + 2;
                res = Math.max(res, chainSize);
            }
            else {
                res = Math.max(res, cnt);
            }
        }
        return res;
    }
}