1981. 最小化目标值与所选元素的差
给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。
从矩阵的 每一行 中选择一个整数,你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。
返回 最小的绝对差 。
a 和 b 两数字的 绝对差 是 a - b 的绝对值。
示例 1:
1
2
3
4
5
6
7
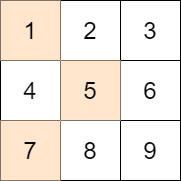
| 输入:mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
输出:0
解释:一种可能的最优选择方案是:
- 第一行选出 1
- 第二行选出 5
- 第三行选出 7
所选元素的和是 13 ,等于目标值,所以绝对差是 0 。
|
示例 2:

1
2
3
4
5
6
7
| 输入:mat = [[1],[2],[3]], target = 100
输出:94
解释:唯一一种选择方案是:
- 第一行选出 1
- 第二行选出 2
- 第三行选出 3
所选元素的和是 6 ,绝对差是 94 。
|
示例 3:

1
2
3
4
| 输入:mat = [[1,2,9,8,7]], target = 6
输出:1
解释:最优的选择方案是选出第一行的 7 。
绝对差是 1 。
|
提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 701 <= mat[i][j] <= 701 <= target <= 800
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int minimizeTheDifference(int[][] mat, int target) {
int m = mat.length, n = mat[0].length;
int f[][] = new int[m+1][6000];
f[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
for (int k = 0; k <= 5000; k++) {
f[i+1][k+mat[i][j]] = Math.max(f[i+1][k+mat[i][j]], f[i][k]);
}
}
}
int res = 5000;
for (int i = 0; i <= 5000; i++) {
if (f[m][i] == 1) res = Math.min(res, Math.abs(i-target));
}
return res;
}
}
|



