1594. 矩阵的最大非负积(1807)
给你一个大小为 m x n 的矩阵 grid 。最初,你位于左上角 (0, 0) ,每一步,你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (m - 1, n - 1) 结束的所有路径中,找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对 10^9 + 7 取余 的结果。如果最大积为 负数 ,则返回 -1 。
**注意,**取余是在得到最大积之后执行的。
示例 1:
1
2
3
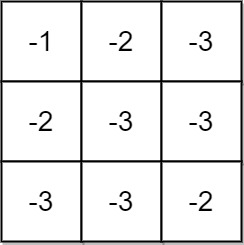
| 输入:grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
输出:-1
解释:从 (0, 0) 到 (2, 2) 的路径中无法得到非负积,所以返回 -1 。
|
示例 2:
1
2
3
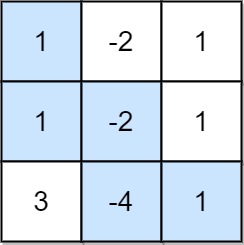
| 输入:grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
输出:8
解释:最大非负积对应的路径如图所示 (1 * 1 * -2 * -4 * 1 = 8)
|
示例 3:
1
2
3
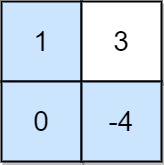
| 输入:grid = [[1,3],[0,-4]]
输出:0
解释:最大非负积对应的路径如图所示 (1 * 0 * -4 = 0)
|
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 15-4 <= grid[i][j] <= 4
思路:最小值和最大值两个dp矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int maxProductPath(int[][] grid) {
int m = grid.length, n = grid[0].length, MOD = (int)1e9+7;
long f[][][] = new long[m][n][2];
f[0][0][0] = f[0][0][1] = grid[0][0];
for (int i = 1; i < m; i++) {
f[i][0][0] = f[i][0][1] = f[i-1][0][0]*grid[i][0];
}
for (int i = 1; i < n; i++) {
f[0][i][0] = f[0][i][1] = f[0][i-1][0]*grid[0][i];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (grid[i][j] >= 0) {
f[i][j][0] = Math.min(f[i-1][j][0]*grid[i][j], f[i][j-1][0]*grid[i][j]);
f[i][j][1] = Math.max(f[i-1][j][1]*grid[i][j], f[i][j-1][1]*grid[i][j]);
}
else {
f[i][j][0] = Math.min(f[i-1][j][1]*grid[i][j], f[i][j-1][1]*grid[i][j]);
f[i][j][1] = Math.max(f[i-1][j][0]*grid[i][j], f[i][j-1][0]*grid[i][j]);
}
}
}
if (f[m-1][n-1][1] < 0) return -1;
return (int)(f[m-1][n-1][1]%MOD);
}
}
|



