差分数组

1
2
3
4
a[0] a[1] a[2] a[3] a[4] (0)
差分数组: a[0] a[1]-a[0] a[2]-a[1] a[3]-a[2] a[4]-a[3] (-a[4])
对差分数组求前缀和: a[0] a[1] a[2] a[3] a[4] (0)
// 考虑末尾0(-a[4])，那么差分数组之和sum=0

前缀和就是离散版本的“求积分”，差分数组就是离散版本的“求微分”

形成目标数组的子数组最少增加次数

给你一个整数数组 target 和一个数组 initial ，initial 数组与 target 数组有同样的维度，且一开始全部为 0 。

请你返回从 initial 得到 target 的最少操作次数，每次操作需遵循以下规则：

  • 在 initial 中选择 任意 子数组，并将子数组中每个元素增加 1 。

答案保证在 32 位有符号整数以内。

示例 1：

1
2
3
4
5
6
7
输入：target = [1,2,3,2,1]
输出：3
解释：我们需要至少 3 次操作从 intial 数组得到 target 数组。
[0,0,0,0,0] 将下标为 0 到 4 的元素（包含二者）加 1 。
[1,1,1,1,1] 将下标为 1 到 3 的元素（包含二者）加 1 。
[1,2,2,2,1] 将下表为 2 的元素增加 1 。
[1,2,3,2,1] 得到了目标数组。

示例 2：

1
2
3
输入：target = [3,1,1,2]
输出：4
解释：(initial)[0,0,0,0] -> [1,1,1,1] -> [1,1,1,2] -> [2,1,1,2] -> [3,1,1,2] (target) 。

示例 3：

1
2
3
4
输入：target = [3,1,5,4,2]
输出：7
解释：(initial)[0,0,0,0,0] -> [1,1,1,1,1] -> [2,1,1,1,1] -> [3,1,1,1,1] 
            -> [3,1,2,2,2] -> [3,1,3,3,2] -> [3,1,4,4,2] -> [3,1,5,4,2] (target)。

示例 4：

1
2
输入：target = [1,1,1,1]
输出：1

提示：

  • 1 <= target.length <= 10^5
  • 1 <= target[i] <= 10^5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int minNumberOperations(int[] target) {
        int n = target.length, d[] = new int[n+1], res = 0;
        d[0] = target[0];
        for (int i = 1; i < n; i++) {
            d[i] = target[i] - target[i-1];
        }
        d[n] = -target[n-1];
        for (int dd : d) {
            if (dd > 0) res += dd;
        }
        return res;
    }
}

使数组等于目标数组所需的最少操作次数

给你两个长度相同的正整数数组 nums 和 target。

在一次操作中，你可以选择 nums 的任何

子数组

，并将该子数组内的每个元素的值增加或减少 1。

返回使 nums 数组变为 target 数组所需的 最少 操作次数。

示例 1：

输入： nums = [3,5,1,2], target = [4,6,2,4]

输出： 2

解释：

执行以下操作可以使 nums 等于 target：
- nums[0..3] 增加 1，nums = [4,6,2,3]。
- nums[3..3] 增加 1，nums = [4,6,2,4]。

示例 2：

输入： nums = [1,3,2], target = [2,1,4]

输出： 5

解释：

执行以下操作可以使 nums 等于 target：
- nums[0..0] 增加 1，nums = [2,3,2]。
- nums[1..1] 减少 1，nums = [2,2,2]。
- nums[1..1] 减少 1，nums = [2,1,2]。
- nums[2..2] 增加 1，nums = [2,1,3]。
- nums[2..2] 增加 1，nums = [2,1,4]。

提示：

  • 1 <= nums.length == target.length <= 10^5
  • 1 <= nums[i], target[i] <= 10^8
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public long minimumOperations(int[] nums, int[] target) {
        int n = target.length, diff[] = new int[n], d[] = new int[n+1];
        long res = 0;
        for (int i = 0; i < n; i++) diff[i] = nums[i] - target[i];
        d[0] = diff[0];
        for (int i = 1; i < n; i++) {
            d[i] = diff[i] - diff[i-1];
        }
        d[n] = -diff[n-1];
        for (int dd : d) {
            if (dd > 0) res += dd;
        }
        return res;
    }
}

二维差分数组

假设对于原矩阵，给一个左上角grid[l][u]，右下角grid[r][d]的子矩阵的元素都添加一

那么对于差分数组diff[][]来说，相当于：

1
2
3
4
5
6
// 是否要+1取决于需求，都可以
// l r u d分别表示左右上下
diff[l][u]++;  // 添加左上角到结束的矩阵（差分的特点就是，+1相当于加到了结束，联想一维的情况）
diff[r+1][u]--;  // 删除右上角到结束的矩阵
diff[l][d+1]--;  // 删除左下角到结束的矩阵
diff[r+1][d+1]++;  // 添加右下角到结束的矩阵（因为两次删除了重复的区域，所以要加回来）

比如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
// 原矩阵
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
// 给一个左上角`grid[1][1]`，右下角`grid[3][3]`的子矩阵的元素都添加
0 0 0 0 0 0
0 1 1 1 0 0
0 1 1 1 0 0
0 1 1 1 0 0
0 0 0 0 0 0
0 0 0 0 0 0
// 对应差分数组
0 0 0 0 0 0
0 1 0 0 -1 0
0 0 0 0 0 0
0 0 0 0 0 0
0 -1 0 0 1 0
0 0 0 0 0 0

用邮票贴满网格图

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下 限制 和 要求 ：

  1. 覆盖所有 空 格子。
  2. 不覆盖任何 被占据 的格子。
  3. 我们可以放入任意数目的邮票。
  4. 邮票可以相互有 重叠 部分。
  5. 邮票不允许 旋转 。
  6. 邮票必须完全在矩阵 内 。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

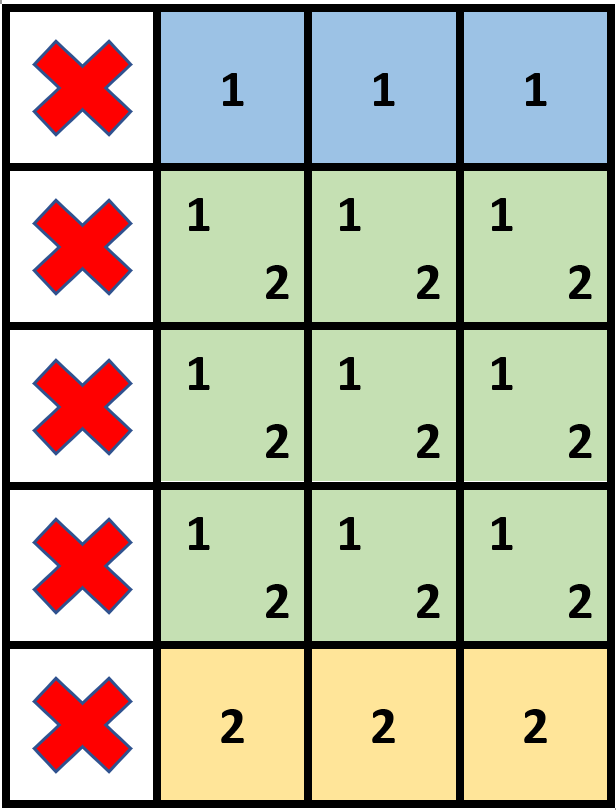
示例 1：

1
2
3
输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

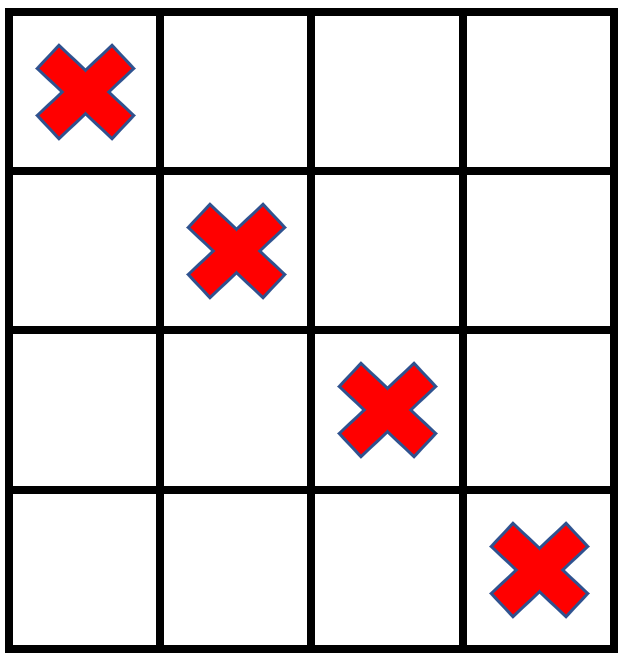
示例 2：

1
2
3
输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。

提示：

  • m == grid.length
  • n == grid[r].length
  • 1 <= m, n <= 10^5
  • 1 <= m * n <= 2 * 10^5
  • grid[r][c] 要么是 0 ，要么是 1 。
  • 1 <= stampHeight, stampWidth <= 10^5

二维前缀和+二维差分数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) {
        int m = grid.length, n = grid[0].length, sum[][] = new int[m+1][n+1], diff[][] = new int[m+2][n+2];
        // 计算二维前缀和
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                sum[i+1][j+1] = grid[i][j] + sum[i+1][j] + sum[i][j+1] - sum[i][j];
            }
        }
        // 通过差分数组涂鸦所有可以涂鸦的区块
        for (int i = 0; i < m - stampHeight + 1; i++) {
            for (int j = 0; j < n - stampWidth + 1; j++) {
                int l = i, r = i+stampHeight, u = j, d = j+stampWidth;  // 这里r和d已经相当于+1了
                if (sum[r][d] - sum[l][d] - sum[r][u] + sum[l][u] == 0) {  // 判断当前区块是否可以涂鸦
                    // 为了方便最后一步计算，不需要考虑0的情况，这边都要+1偏移，对应diff数组大小为m+2和n+2
                    diff[l+1][u+1]++;  // 添加左上角到结束的矩阵（差分的特点就是，+1相当于加到了结束，联想一维的情况）
                    diff[r+1][u+1]--;  // 删除右上角到结束的矩阵
                    diff[l+1][d+1]--;  // 删除左下角到结束的矩阵
                    diff[r+1][d+1]++;  // 添加右下角到结束的矩阵（因为两次删除了重复的区域，所以要加回来）
                }
            }
        }
        // 通过差分数组和原数组判断是否未被涂鸦
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                diff[i+1][j+1] += diff[i+1][j] + diff[i][j+1] - diff[i][j];  // 重叠了多少涂鸦，值就是几
                if (grid[i][j] == 0 && diff[i+1][j+1] == 0) return false;
            }
        }
        return true;
    }
}