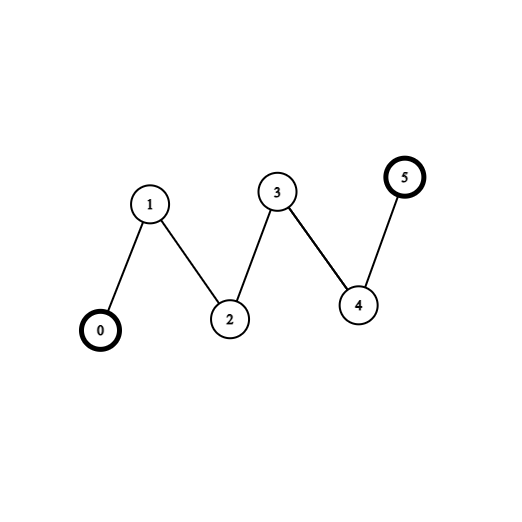
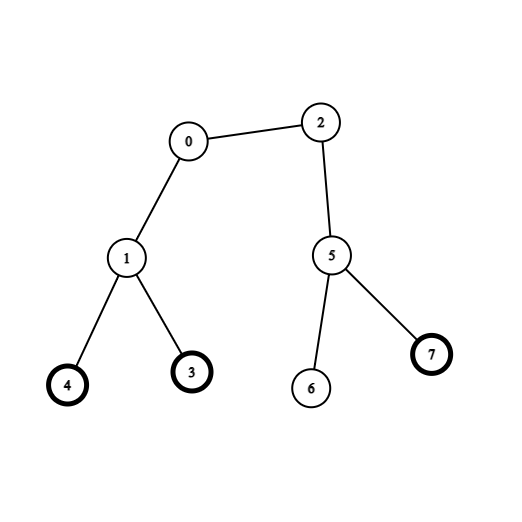
拓扑排序

概念

拓扑排序是一种在有向图中对节点进行排序的算法，其中每个节点表示一个任务或事件，而有向边表示任务间的依赖关系。拓扑排序可以帮助我们找到一种满足依赖关系的节点排列顺序，从而确保所有依赖关系得到满足。

概述

拓扑排序通常用于解决有向无环图（DAG）中的任务调度、依赖分析、编译顺序等问题。在一个有向图中，每个节点代表一个任务，而有向边代表任务间的依赖关系。拓扑排序的目标是找到一种节点排列，使得每个节点都排在它的后继节点之前，从而满足所有的依赖关系。

基于BFS的拓扑排序算法步骤

  1. 初始化一个队列，将所有入度为 0 的节点入队。
  2. 当队列不为空时，执行以下操作：
    • 从队列中弹出一个节点，将其添加到结果列表中。
    • 遍历该节点的所有后继节点（邻居节点）：
      • 将后继节点的入度减一。
      • 如果后继节点的入度变为 0，则将其入队。
  3. 重复步骤 2，直到队列为空。

基于DFS的拓扑排序算法步骤

  1. 选择一个没有入边的节点作为起点。
  2. 对起点节点进行DFS遍历，将遍历过程中的节点按照逆序加入到结果列表中。
  3. 重复步骤 1 和步骤 2，直到所有节点都被遍历过。

课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

  • 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

  • 1 <= numCourses <= 2000
  • 0 <= prerequisites.length <= 5000
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • prerequisites[i] 中的所有课程对 互不相同

bfs

如果有环，那么这个环的节点的入度永远不会为0，就不会被加入队列，所以count会小于numCourses

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int n = prerequisites.length, degree[] = new int[numCourses];
        ArrayList<Integer> edges[] = new ArrayList[numCourses];
        for(int i = 0; i < numCourses; i++) edges[i] = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            int x = prerequisites[i][0], y = prerequisites[i][1];
            degree[x] += 1;
            edges[y].add(x);
        }
        Deque<Integer> q = new LinkedList<>();
        int count = 0;
        for (int i = 0; i < numCourses; i++) {
            if (degree[i] == 0) q.offer(i);
        }
        while (!q.isEmpty()) {
            int poll = q.poll();
            count += 1;
            for (int x : edges[poll]) {
                degree[x] -= 1;
                if (degree[x] == 0) q.offer(x);
            }
        }
        return count == numCourses;
    }
}

课程表 II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

  • 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。

返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

示例 1：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0]]
输出：[0,1]
解释：总共有 2 门课程。要学习课程 1，你需要先完成课程 0。因此，正确的课程顺序为 [0,1] 。

示例 2：

1
2
3
4
输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出：[0,2,1,3]
解释：总共有 4 门课程。要学习课程 3，你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此，一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。

示例 3：

1
2
输入：numCourses = 1, prerequisites = []
输出：[0]

提示：

  • 1 <= numCourses <= 2000
  • 0 <= prerequisites.length <= numCourses * (numCourses - 1)
  • prerequisites[i].length == 2
  • 0 <= ai, bi < numCourses
  • ai != bi
  • 所有[ai, bi] 互不相同

dfs

dfs需要保存节点的状态，用vis表示，0表示未被访问，1表示正在访问，2表示访问过

并用一个cycle布尔值来表示是否存在环

如果在dfs的过程中访问到了vis为1的节点，那么说明存在换，把cycle置为true

这题还需要返回路径，所以我们需要记录路径，dfs的路径最后还需要reverse才是答案。这题用string记录res不太好，直接用int[]记录更好（路径的长度是固定的）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    String res = "";
    boolean cycle = false;
    public int[] findOrder(int numCourses, int[][] prerequisites) {
        int n = prerequisites.length, degree[] = new int[numCourses];
        ArrayList<Integer> edges[] = new ArrayList[numCourses];
        for(int i = 0; i < numCourses; i++) edges[i] = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            int x = prerequisites[i][0], y = prerequisites[i][1];
            degree[x] += 1;
            edges[y].add(x);
        }
        int vis[] = new int[numCourses];
        for (int i = 0; i < numCourses && !cycle; i++) {
            if (vis[i] == 0) {
                dfs(i, edges, vis);
            }
        }
        if (cycle) return new int[]{};
        int dfsRes[] = Arrays.stream(res.split(" ")).mapToInt(i -> Integer.valueOf(i)).toArray();
        int finalRes[] = IntStream.range(0, dfsRes.length).map(i -> dfsRes[dfsRes.length-1-i]).toArray();
        return finalRes;
    }
    public void dfs(int cur, ArrayList<Integer>[] edges, int[] vis) {
        vis[cur] = 1;
        if (cycle) return;
        for (int x : edges[cur]) {
            if (vis[x] == 0) {
                dfs(x, edges, vis);
            }
            else if (vis[x] == 1) {
                cycle = true;
                return;
            }
        }
        vis[cur] = 2;
        res += cur + " ";
    }
}

外星文字典

现有一种使用英语字母的外星文语言，这门语言的字母顺序与英语顺序不同。

给定一个字符串列表 words ，作为这门语言的词典，words 中的字符串已经 按这门新语言的字母顺序进行了排序 。

请你根据该词典还原出此语言中已知的字母顺序，并 按字母递增顺序 排列。若不存在合法字母顺序，返回 "" 。若存在多种可能的合法字母顺序，返回其中 任意一种 顺序即可。

字符串 s 字典顺序小于 字符串 t 有两种情况：

  • 在第一个不同字母处，如果 s 中的字母在这门外星语言的字母顺序中位于 t 中字母之前，那么 s 的字典顺序小于 t 。
  • 如果前面 min(s.length, t.length) 字母都相同，那么 s.length < t.length 时，s 的字典顺序也小于 t 。

示例 1：

1
2
输入：words = ["wrt","wrf","er","ett","rftt"]
输出："wertf"

示例 2：

1
2
输入：words = ["z","x"]
输出："zx"

示例 3：

1
2
3
输入：words = ["z","x","z"]
输出：""
解释：不存在合法字母顺序，因此返回 "" 。

提示：

  • 1 <= words.length <= 100
  • 1 <= words[i].length <= 100
  • words[i] 仅由小写英文字母组成

拓扑排序+bfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class TopoSortBfs {  // 拓扑排序+bfs
    HashMap<Character, List<Character>> map = new HashMap<>();  // 存储有向边
    HashMap<Character, Integer> inter = new HashMap<>();  // 存储每个点入度（如果有）
    public String alienOrder(String[] words) {
        int len = words.length;
        String ans = "";
        for (String word : words) {  // 将所有出现的char存入map（防止最后结果不完整）
            for (char c : word.toCharArray()) {
                map.putIfAbsent(c, new ArrayList<>());
            }
        }
        for (int i = 1; i < len; i++) {  // 建图（map和inter：边和入度）
            String last = words[i-1];
            String cur = words[i];
            int minLen = Math.min(last.length(), cur.length());
            int index = 0;
            while (index < minLen) {
                if (last.charAt(index) != cur.charAt(index)) {
                    map.get(last.charAt(index)).add(cur.charAt(index));
                    inter.put(cur.charAt(index), inter.getOrDefault(cur.charAt(index), 0)+1);
                    break;
                }
                ++index;
            }
            if (index == minLen && last.length() > cur.length())
                return "";
        }
        Queue<Character> q = new ArrayDeque<>();
        Set<Character> keys = map.keySet();
        for (Character key : keys) {  // 把所有入度为0的点先拿出来，放入queue
            if (!inter.containsKey(key))
                q.offer(key);
        }
        while (!q.isEmpty()) {  // 不断地从queue拿取首部
            Character poll = q.poll();
            ans += poll;
            // System.out.println(poll);
            List<Character> cs = map.get(poll);  // 该点的边对应的所有终点
//            if (cs == null) continue;
            for (int i = 0; i < cs.size(); i++) {  // 把所有终点的入度都-1
                Character c = cs.get(i);
                inter.put(c, inter.get(c)-1);
                if (inter.get(c) == 0)  // 如果入度为0，则加入queue
                    q.offer(c);
            }
        }
        return ans.length() == map.size() ? ans : "";
    }
}

拓扑排序+dfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class TopoSortDfs {  // 拓扑排序+dfs
    int VISITING = 1, VISITED = 2;
    HashMap<Character, List<Character>> map = new HashMap<>();
    HashMap<Character, Integer> state = new HashMap<>();
    String ans = "";
    public String alienOrder(String[] words) {
        int len = words.length;
        for (String word : words) {
            for (char c : word.toCharArray()) {
                map.putIfAbsent(c, new ArrayList<>());
                state.put(c, 0);
            }
        }
        for (int i = 1; i < len; i++) {
            String last = words[i-1];
            String cur = words[i];
            int minLen = Math.min(last.length(), cur.length());
            int index = 0;
            while (index < minLen) {
                if (last.charAt(index) != cur.charAt(index)) {
                    map.get(last.charAt(index)).add(cur.charAt(index));
                    break;
                }
                ++index;
            }
            if (index == minLen && last.length() > cur.length())
                return "";
        }
        Set<Character> keys = map.keySet();
        for (Character key : keys) {
            if (state.get(key) == 0)  // 如果未访问该点，那么dfs
                dfs(key);
        }
        return ans.length() == map.size() ? new StringBuilder(ans).reverse().toString() : "";
    }
    public void dfs(Character cur) {
        state.put(cur, VISITING);  // 设置当前节点为正在访问
        List<Character> cs = map.get(cur);  // 获取边的所有终点
        for (int i = 0; i < cs.size(); i++) {
            Character c = cs.get(i);
            if (state.get(c) == 0) {  // 如果未访问该终点，那么dfs
                dfs(c);
            }
            else if (state.get(c) == VISITING) {  // 如果正在访问说明，存在环，直接返回
                return;
            }
            // 还有一种情况是等于VISITED，已访问过该终点，说明已经加入到ans中，则不用管即可
        }
        ans += cur;  // ans不是最终的结果，最后需要reverse
        state.put(cur, VISITED);
    }
}

收集树中金币

给你一个 n 个节点的无向无根树，节点编号从 0 到 n - 1 。给你整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间有一条边。再给你一个长度为 n 的数组 coins ，其中 coins[i] 可能为 0 也可能为 1 ，1 表示节点 i 处有一个金币。

一开始，你需要选择树中任意一个节点出发。你可以执行下述操作任意次：

  • 收集距离当前节点距离为 2 以内的所有金币，或者
  • 移动到树中一个相邻节点。

你需要收集树中所有的金币，并且回到出发节点，请你返回最少经过的边数。

如果你多次经过一条边，每一次经过都会给答案加一。

示例 1：

1
2
3
输入：coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：从节点 2 出发，收集节点 0 处的金币，移动到节点 3 ，收集节点 5 处的金币，然后移动回节点 2 。

示例 2：

1
2
3
输入：coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
输出：2
解释：从节点 0 出发，收集节点 4 和 3 处的金币，移动到节点 2 处，收集节点 7 处的金币，移动回节点 0 。

提示：

  • n == coins.length
  • 1 <= n <= 3 * 10^4
  • 0 <= coins[i] <= 1
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges 表示一棵合法的树。

拓扑排序 + 拓扑排序 + bfs

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class Solution {
    public int collectTheCoins(int[] coins, int[][] edges) {
        int n = coins.length, res = 0, degree[] = new int[n];
        List<Integer> g[] = new ArrayList[n];
        Arrays.setAll(g, i -> new ArrayList<>());
        for (int e[] : edges) {
            int x = e[0], y = e[1];
            g[x].add(y); g[y].add(x);
            degree[x] += 1; degree[y] += 1;
        }
        Deque<Integer> q = new LinkedList<>();
        // 拓扑排序，bfs删除所有没有金币的叶子节点
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1 && coins[i] == 0) {
                q.offer(i);
            }
        }
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int poll = q.poll();
                for (int to : g[poll]) {
                    if (degree[to] == 0) continue;  // degree == 0 代表被访问过的叶子节点
                    degree[to] -= 1;
                    degree[poll] -= 1;
                }
            }
            for (int i = 0; i < n; i++) {
                if (degree[i] == 1 && coins[i] == 0) {
                    q.offer(i);
                }
            }
        }
        // 还是bfs拓扑排序，继续进行两轮叶子节点的删除，删除后剩下的节点就是题目中必须要经过的节点
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1) {
                q.offer(i);
            }
        }
        int count = 0;
        while (!q.isEmpty() && count++ < 2) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int poll = q.poll();
                for (int to : g[poll]) {
                    if (degree[to] == 0) continue;
                    degree[to] -= 1;
                    degree[poll] -= 1;
                }
            }
            for (int i = 0; i < n; i++) {
                if (degree[i] == 1) {
                    q.offer(i);
                }
            }
        }
        if (count < 2) return 0;
        q.clear();
        // 在剩下的节点中，用普通bfs寻找剩下节点的边数，答案等于边数*2
        // 也可以省略这一步，用最开始所有边数(n-1) - 上面拓扑遍历到的边数，就是res
        for (int i = 0; i < n; i++) {
            // 随便找一个起始点
            if (degree[i] != 0) {
                q.offer(i);
                break;
            }
        }
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int poll = q.poll();
                for (int to : g[poll]) {
                    if (degree[to] == 0) continue;
                    degree[to] -= 1;
                    degree[poll] -= 1;
                    res += 2;
                    q.offer(to);
                }
            }
        }
        return res;
    }
}

相关题目