Floyd算法

概念

Floyd算法，也称为Floyd-Warshall算法，是一种用于求解图中所有顶点对之间最短路径的算法。

它是一种动态规划算法，适用于有向图或带权图，可以处理负权边（但不能包含负权回路，负权回路会导致无限小路径）。

伪代码

1
2
3
4
5
for(k : V)
  for(i : V)
    for(j : V)
      if(d(i, k) + d(k, j) < d(i, j))
        d(i, j) = d(i, k) + d(k, j)

算法过程

该算法的本质是动态规划，以状态转移方程的形式描述如下，其中 dp[k][i][j] 表示 经过前 k 个顶点的松弛，得到的顶点 i 到顶点 j 的最短路径长度 。注意第一维的 k 表示 k 个顶点，第二维和第三维表示具体的顶点。

  1. 定义: dp[k][i][j] 表示经过前 k 个顶点的松弛，得到的顶点 i 到顶点 j 的最短路径长度。
  2. 边界: dp[0][i][j] = i == j ? 0 : (g[i][j] == 0 ? Inf : g[i][j])
  3. 递推: dp[k][i][j] = min{dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j]}

最短路径 不经过 第 k 个顶点 (顶点 k ): dp[k][i][j] = dp[k-1][i][j]

最短路径 经过 第 k 个顶点 (顶点 k ): dp[k][i][j] = dp[k-1][i][k] + dp[k-1][k][j]

由于 k 的每次遍历是独立的，所以可以去掉这个维度，节省空间

dp[i][j] = min{dp[i][j], dp[i][k] + dp[k][j]}

课程表 IV

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你 必须 先选 ai 课程。

  • 有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。

先决条件也可以是 间接 的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。

你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。

返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

示例 1：

1
2
3
输入：numCourses = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
输出：[false,true]
解释：课程 0 不是课程 1 的先修课程，但课程 1 是课程 0 的先修课程。

示例 2：

1
2
3
输入：numCourses = 2, prerequisites = [], queries = [[1,0],[0,1]]
输出：[false,false]
解释：没有先修课程对，所以每门课程之间是独立的。

示例 3：

1
2
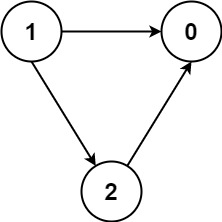
输入：numCourses = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
输出：[true,true]

提示：

  • 2 <= numCourses <= 100
  • 0 <= prerequisites.length <= (numCourses * (numCourses - 1) / 2)
  • prerequisites[i].length == 2
  • 0 <= ai, bi <= n - 1
  • ai != bi
  • 每一对 [ai, bi] 都 不同
  • 先修课程图中没有环。
  • 1 <= queries.length <= 10^4
  • 0 <= ui, vi <= n - 1
  • ui != vi

Floyd三维dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        List<Boolean> res = new ArrayList<>();
        int dp[][][] = new int[numCourses+1][numCourses][numCourses];
        for (int i = 0; i < numCourses; i++) {
            for (int j = 0; j < numCourses; j++) {
                if (i == j) {
                    dp[0][i][j] = 0;
                }
                else {
                    dp[0][i][j] = 200;
                }
            }
        }
        for (int p[] : prerequisites) {
            int x = p[0], y = p[1];
            dp[0][x][y] = 1;
        }
        for (int k = 0; k < numCourses; k++) {
            for (int i = 0; i < numCourses; i++) {
                for (int j = 0; j < numCourses; j++) {
                    dp[k+1][i][j] = Math.min(dp[k][i][j], dp[k][i][k] + dp[k][k][j]);
                }
            }
        }
        for (int q[] : queries) {
            int x = q[0], y = q[1];
            res.add(dp[numCourses][x][y] < 200);
        }
        return res;
    }
}

Floyd二维dp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public List<Boolean> checkIfPrerequisite(int numCourses, int[][] prerequisites, int[][] queries) {
        List<Boolean> res = new ArrayList<>();
        int dp[][] = new int[numCourses][numCourses];
        for (int i = 0; i < numCourses; i++) {
            for (int j = 0; j < numCourses; j++) {
                dp[i][j] = i == j ? 0 : 200;
            }
        }
        for (int p[] : prerequisites) {
            dp[p[0]][p[1]] = 1;
        }
        for (int k = 0; k < numCourses; k++) {
            for (int i = 0; i < numCourses; i++) {
                for (int j = 0; j < numCourses; j++) {
                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
                }
            }
        }
        for (int q[] : queries) {
            res.add(dp[q[0]][q[1]] < 200);
        }
        return res;
    }
}

Floyd + BitSet优化

  • 2101. 引爆最多的炸弹(1880)
    题解

    给你一个炸弹列表。一个炸弹的 爆炸范围 定义为以炸弹为圆心的一个圆。

    炸弹用一个下标从 0 开始的二维整数数组 bombs 表示，其中 bombs[i] = [xi, yi, ri] 。xi 和 yi 表示第 i 个炸弹的 X 和 Y 坐标，ri 表示爆炸范围的 半径 。

    你需要选择引爆 一个 炸弹。当这个炸弹被引爆时，所有 在它爆炸范围内的炸弹都会被引爆，这些炸弹会进一步将它们爆炸范围内的其他炸弹引爆。

    给你数组 bombs ，请你返回在引爆 一个 炸弹的前提下，最多 能引爆的炸弹数目。

    示例 1：

    1
    2
    3
    4
    5
    6
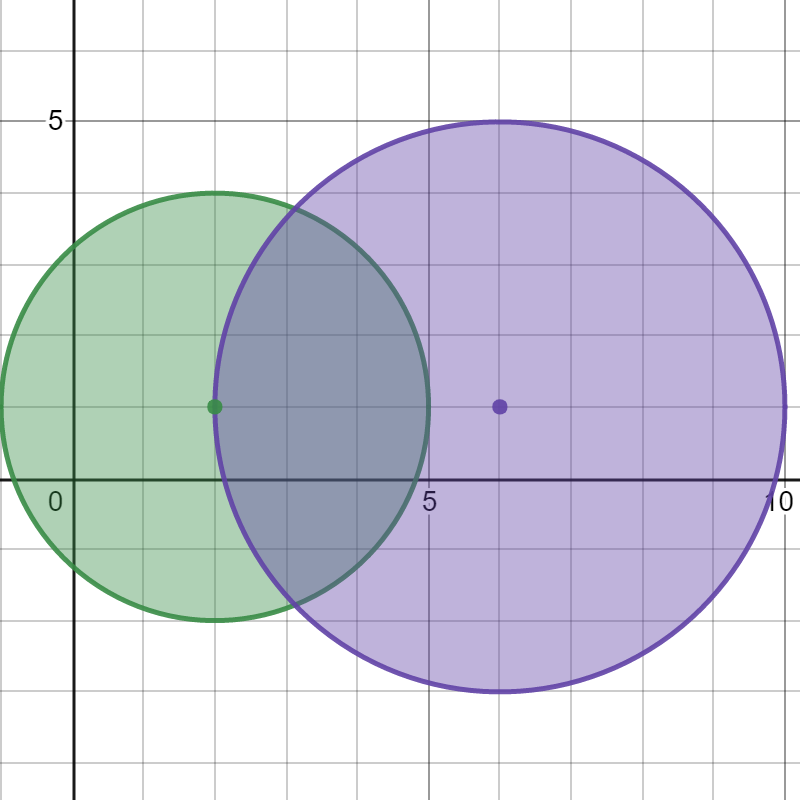
    7
    输入：bombs = [[2,1,3],[6,1,4]]
    输出：2
    解释：
    上图展示了 2 个炸弹的位置和爆炸范围。
    如果我们引爆左边的炸弹，右边的炸弹不会被影响。
    但如果我们引爆右边的炸弹，两个炸弹都会爆炸。
    所以最多能引爆的炸弹数目是 max(1, 2) = 2 。

    示例 2：

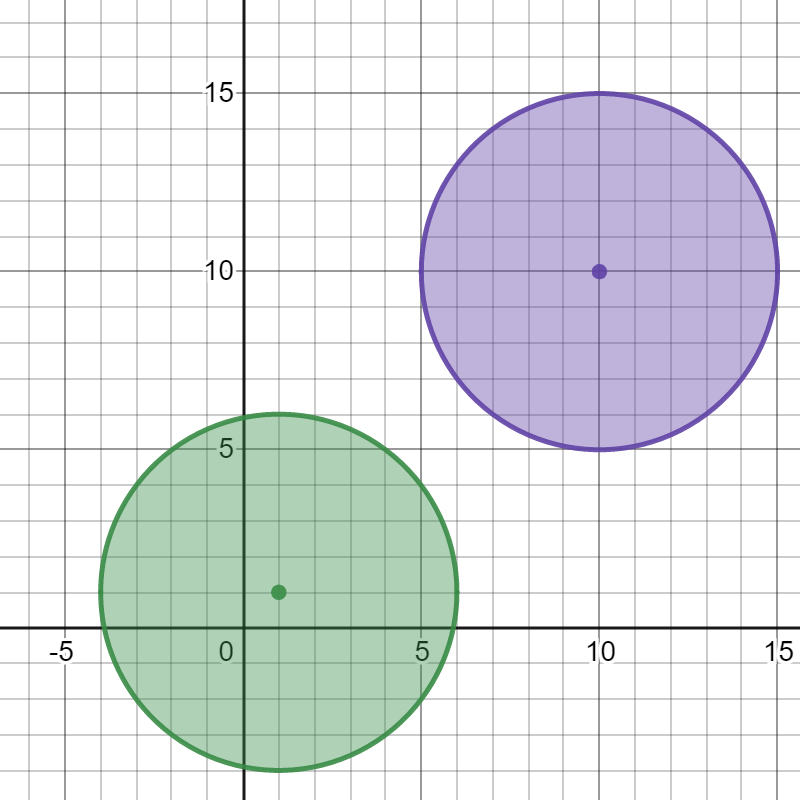
    1
    2
    3
    4
    输入：bombs = [[1,1,5],[10,10,5]]
    输出：1
    解释：
    引爆任意一个炸弹都不会引爆另一个炸弹。所以最多能引爆的炸弹数目为 1 。

    示例 3：

    1
    2
    3
    4
    5
    6
    7
    8
    输入：bombs = [[1,2,3],[2,3,1],[3,4,2],[4,5,3],[5,6,4]]
    输出：5
    解释：
    最佳引爆炸弹为炸弹 0 ，因为：
    - 炸弹 0 引爆炸弹 1 和 2 。红色圆表示炸弹 0 的爆炸范围。
    - 炸弹 2 引爆炸弹 3 。蓝色圆表示炸弹 2 的爆炸范围。
    - 炸弹 3 引爆炸弹 4 。绿色圆表示炸弹 3 的爆炸范围。
    所以总共有 5 个炸弹被引爆。

    提示：

    • 1 <= bombs.length <= 100
    • bombs[i].length == 3
    • 1 <= xi, yi, ri <= 10^5
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    class Solution {
        public int maximumDetonation(int[][] bombs) {
            int n = bombs.length, res = 0;
            BitSet set[] = new BitSet[n];
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    long a = bombs[j][0] - bombs[i][0], b = bombs[j][1] - bombs[i][1], r1 = bombs[i][2], r2 = bombs[j][2];
                    if (a*a + b*b <= r1*r1) set[i].set(j);
                    if (a*a + b*b <= r2*r2) set[j].set(i);
                }
            }
            for (int k = 0; k < n; k++) {
                for (BitSet b : set) {
                    if (b.get(k)) {
                        b.or(set[k]);
                    }
                }
            }
            for (BitSet b : set) {
                res = Math.max(res, b.cardinality());
            }
            return res;
        }
    }