建图是一个机械劳作
邻接矩阵
邻接矩阵是一个二维数组,其行和列都对应图中的顶点。如果顶点i和顶点j之间存在边,则矩阵中的i,j 位置的元素为1(对于无权图),或为边的权重(对于有权图)。如果i=j,则通常为0,表示顶点不会与自己相连
一般来说,题目给出的都是邻接矩阵的形式。
例如743. 网络延迟时间
这个题目就是给你一个列表 times,表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi),其中 ui 是源节点,vi 是目标节点, wi 是一个信号从源节点传递到目标节点的时间。
本篇主要讨论如何将邻接矩阵转换成其它的存图方式
邻接表
邻接表是表示图中顶点之间相邻关系的一种方式。对于图中的每一个顶点,邻接表包含了与该顶点直接相连的所有顶点的列表。
1 2 3 4 5 6 7 8 public int networkDelayTime (int [][] times, int n, int k) { List<int []> g[] = new ArrayList [n]; Arrays.setAll(g, i -> new ArrayList <>()); for (int [] e : times) { int u = e[0 ]-1 , v = e[1 ]-1 , w = e[2 ]; g[u].add(new int []{v, w}); } }
链式向前星
以Dinic算法中的链式向前星建图为例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 int n, m, s, t, lv[], cur[], heads[], nexts[], tos[], weights[];public Dinic (int n, int s, int t, int edges[][]) { this .n = n; this .s = s; this .t = t; lv = new int [n+1 ]; heads = new int [n+1 ]; cur = new int [n+1 ]; m = edges.length; int edgeNum = 1 ; tos = new int [2 *m + 2 ]; nexts = new int [2 *m + 2 ]; weights = new int [2 *m + 2 ]; for (int [] edge : edges) { int u = edge[0 ], v = edge[1 ], w = edge[2 ]; ++edgeNum; nexts[edgeNum] = heads[u]; heads[u] = edgeNum; tos[edgeNum] = v; weights[edgeNum] = w; ++edgeNum; nexts[edgeNum] = heads[v]; heads[v] = edgeNum; tos[edgeNum] = u; weights[edgeNum] = 0 ; } }
邻接表,但是同时存无向图和有向图信息
有时候,题目给出的是有向图邻接矩阵,但是我们想通过无向图来进行遍历,同时又想拥有有向图的信息
那么,我们就可以像下面这样建邻接表
1 2 3 4 5 6 7 8 9 10 public int minReorder (int n, int [][] connections) { List<int []> g[] = new ArrayList [n]; int degree[] = new int [n]; Arrays.setAll(g, i -> new ArrayList <>()); for (int connection[] : connections) { int x = connection[0 ], y = connection[1 ]; g[x].add(new int []{y, 1 }); g[y].add(new int []{x, 0 }); } }
n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,以改变交通拥堵的状况。
路线用 connections 表示,其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。
今年,城市 0 将会举办一场大型比赛,很多游客都想前往城市 0 。
请你帮助重新规划路线方向,使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。
题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。
示例 1:
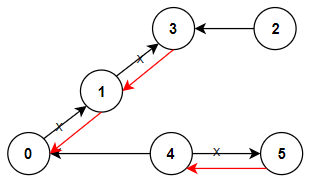
1 2 3 输入:n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]] 输出:3 解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 2:
1 2 3 输入:n = 5, connections = [[1,0],[1,2],[3,2],[3,4]] 输出:2 解释:更改以红色显示的路线的方向,使每个城市都可以到达城市 0 。
示例 3:
1 2 输入:n = 3, connections = [[1,0],[2,0]] 输出:0
提示:
2 <= n <= 5 * 10^4connections.length == n-1connections[i].length == 20 <= connections[i][0], connections[i][1] <= n-1connections[i][0] != connections[i][1]
深度优先遍历
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { List<int []>[] g; public int minReorder (int n, int [][] connections) { g = new ArrayList [n]; int degree[] = new int [n]; Arrays.setAll(g, i -> new ArrayList <>()); for (int connection[] : connections) { int x = connection[0 ], y = connection[1 ]; g[x].add(new int []{y, 1 }); g[y].add(new int []{x, 0 }); } return dfs(-1 , 0 ); } public int dfs (int pre, int cur) { int res = 0 ; for (int nxt[] : g[cur]) { int x = nxt[0 ], y = nxt[1 ]; if (x == pre) continue ; res += y + dfs(cur, x); } return res; } }