algorithm-dp-misc

待分类整理

需要小技巧的动态规划

石子游戏 V（2087

几块石子 排成一行 ，每块石子都有一个关联值，关联值为整数，由数组 stoneValue 给出。

游戏中的每一轮：Alice 会将这行石子分成两个 非空行（即，左侧行和右侧行）；Bob 负责计算每一行的值，即此行中所有石子的值的总和。Bob 会丢弃值最大的行，Alice 的得分为剩下那行的值（每轮累加）。如果两行的值相等，Bob 让 Alice 决定丢弃哪一行。下一轮从剩下的那一行开始。

只 剩下一块石子 时，游戏结束。Alice 的分数最初为 0 。

返回 Alice 能够获得的最大分数 。

示例 1：

输入：stoneValue = [6,2,3,4,5,5]
输出：18
解释：在第一轮中，Alice 将行划分为 [6，2，3]，[4，5，5] 。左行的值是 11 ，右行的值是 14 。Bob 丢弃了右行，Alice 的分数现在是 11 。
在第二轮中，Alice 将行分成 [6]，[2，3] 。这一次 Bob 扔掉了左行，Alice 的分数变成了 16（11 + 5）。
最后一轮 Alice 只能将行分成 [2]，[3] 。Bob 扔掉右行，Alice 的分数现在是 18（16 + 2）。游戏结束，因为这行只剩下一块石头了。

示例 2：

1 2	输入：stoneValue = [7,7,7,7,7,7,7] 输出：28

示例 3：

1 2	输入：stoneValue = [4] 输出：0

提示：

1 <= stoneValue.length <= 500
1 <= stoneValue[i] <= 10^6

记忆化搜索(1750ms)

用记忆化搜索避免重复访问，避免超时

0到n-1的数组一共有n^2个子数组，每个子数组需要一个for循环遍历分割点，所以是n^3的复杂度

n的范围500，勉强通过

class Solution {
    public int stoneGameV(int[] stoneValue) {
        int n = stoneValue.length, sum[] = new int[n];
        for (int i = 0; i < n; i++) {
            sum[i] = (i > 0 ? sum[i-1] : 0) + stoneValue[i];
        }
        return dfs(stoneValue, 0, n-1, sum, new HashMap<Integer, Integer>());
    }
    public int dfs(int[] value, int l, int r, int[] sum, HashMap<Integer, Integer> map) {
        int res = 0, n = value.length;
        if (l == r) return 0;
        int key = l * n + r;
        if (!map.containsKey(key)) {
            for (int i = l; i < r; i++) {
                int leftSum = sum[i] - (l > 0 ? sum[l-1] : 0), rightSum = sum[r] - sum[i];
                if (leftSum <= rightSum) {
                    res = Math.max(res, leftSum + dfs(value, l, i, sum, map));
                }
                if (rightSum <= leftSum) {
                    res = Math.max(res, rightSum + dfs(value, i+1, r, sum, map));
                }
            }
            map.put(key, res);
        }
        return map.get(key);
    }
}

动态规划(280ms)

用int[][] dp取代map

记忆化搜索也是动态规划的一种？

这里其实就是修改了记忆化的方式，把Map改成了数组，看起来像dp

class Solution {
    public int stoneGameV(int[] stoneValue) {
        int n = stoneValue.length, sum[] = new int[n], dp[][] = new int[n][n];
        for (int i = 0; i < n; i++) {
            sum[i] = (i > 0 ? sum[i-1] : 0) + stoneValue[i];
        }
        return dfs(stoneValue, 0, n-1, sum, dp);
    }
    // leftSum < rightSum: dp[l][r] = leftSum + dp[l][i]
    // leftSum > rightSum: dp[l][r] = rightSum + dp[i+1][r]
    // leftSum == rightSum: dp[l][r] = min(leftSum + dp[l][i], rightSum + dp[i+1][r])
    public int dfs(int[] value, int l, int r, int[] sum, int[][] dp) {
        if (l == r) return 0;
        if (dp[l][r] != 0) return dp[l][r];
        for (int i = l; i < r; i++) {
            int leftSum = sum[i] - (l > 0 ? sum[l-1] : 0), rightSum = sum[r] - sum[i];
            if (leftSum <= rightSum) {
                dp[l][r] = Math.max(dp[l][r], leftSum + dfs(value, l, i, sum, dp));
            }
            if (leftSum >= rightSum) {
                dp[l][r] = Math.max(dp[l][r], rightSum + dfs(value, i+1, r, sum, dp));
            }
        }
        return dp[l][r];
    }
}

英雄的力量（2060）

给你一个下标从 0 开始的整数数组 nums ，它表示英雄的能力值。如果我们选出一部分英雄（子序列），这组英雄的力量定义为：

i0 ，i1 ，… ik 表示这组英雄在数组中的下标。那么这组英雄的力量为 max(nums[i0],nums[i1] ... nums[ik])^2 * min(nums[i0],nums[i1] ... nums[ik]) 。

请你返回所有可能的非空英雄组的力量之和。由于答案可能非常大，请你将结果对 10^9 + 7 取余。

示例 1：

输入：nums = [2,1,4]
输出：141
解释：
第 1 组：[2] 的力量为 22 * 2 = 8 。
第 2 组：[1] 的力量为 12 * 1 = 1 。
第 3 组：[4] 的力量为 42 * 4 = 64 。
第 4 组：[2,1] 的力量为 22 * 1 = 4 。
第 5 组：[2,4] 的力量为 42 * 2 = 32 。
第 6 组：[1,4] 的力量为 42 * 1 = 16 。
第 7 组：[2,1,4] 的力量为 42 * 1 = 16 。
所有英雄组的力量之和为 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。

示例 2：

1
2
3

输入：nums = [1,1,1]
输出：7
解释：总共有 7 个英雄组，每一组的力量都是 1 。所以所有英雄组的力量之和为 7 。

提示：

1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9

找规律动态规划

首先对数组从小到大排序

令以n结尾的子数组力量之和的值为dp(n)

对于[a, b, c, d]数组来说

以c结尾的子数组有：

a开头：[a, c], [a, b, c]
b开头：[b, d]

dp(2) = c^2*a*2^1 + c^2*b*2^0 + c^3 = c^2*(a*2^1 + b*2^0 + c)

令 a2 = a*2^1 + b*2^0

则 dp(2) = c^2*(a3 + c)

以d结尾的子数组有：

a开头：[a, d], [a, b, d], [a, c, d], [a, b, c, d]
b开头：[b, d], [b, c, d]
c开头：[c, d]

dp(3) = d^2*a*2^2 + d^2*b*2^1 + d^2*c*2^0 + d^3 = d^2(a*2^2 + b*2^1 + c*2^0 + d)

= d^2(2*(a*2^1 + b*2^0) + c + d)

令 a3 = 2*(a*2^1 + b*2^0) + c = 2*a2 + c

则 dp(3) = d^2(a3 + d)

a(n) = 2*a(n-1) + nums[n]

dp(n) = nums[n]^2(a(n) + nums[n])

class Solution {
    public int sumOfPower(int[] nums) {
        long res = 0, dp = 0;
        int n = nums.length;
        int MOD = (int)1e9 + 7;
        Arrays.sort(nums);
        for (int i = 0; i < n; i++) {
            res = (res + (long)nums[i] * nums[i] % MOD * (dp + nums[i])) % MOD;
            dp = (2 * dp + nums[i]) % MOD;
        }
        return (int)res;
    }
}

常规思路动态规划+前缀和

首先对数组从小到大排序

用dp[i]表示以nums[i]结尾的子序列的最小值之和

因为以nums[i]结尾的子序列可以由以nums[0],…,nums[i−1]结尾的子序列最后加上nums[i]，以及单独一个nums[i]得到

dp[i] = nums[i] + (dp[0] + ... + dp[i-1])

dp[0] + ... + dp[i-1]可以用前缀和来维护：sum[i] = sum[i-1] + dp[i]

dp[i] = nums[i] + sum[i-1]

则以n结尾的子数组力量之和的值为nums[i] * nums[i] * dp[i]

3n 块披萨（2410）

给你一个披萨，它由 3n 块不同大小的部分组成，现在你和你的朋友们需要按照如下规则来分披萨：

你挑选任意一块披萨。
Alice 将会挑选你所选择的披萨逆时针方向的下一块披萨。
Bob 将会挑选你所选择的披萨顺时针方向的下一块披萨。
重复上述过程直到没有披萨剩下。

每一块披萨的大小按顺时针方向由循环数组 slices 表示。

请你返回你可以获得的披萨大小总和的最大值。

示例 1：

1
2
3

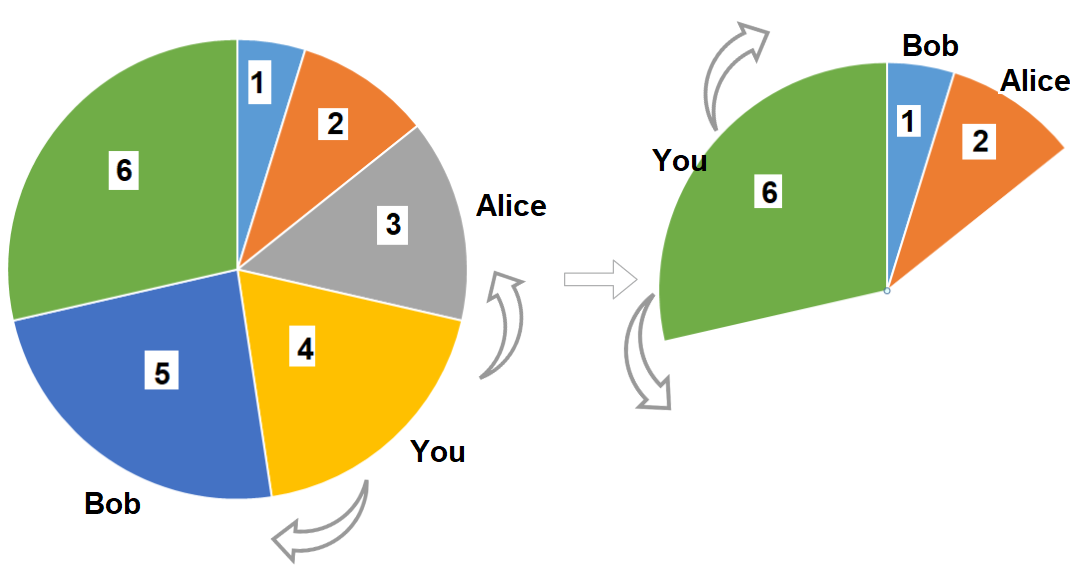
输入：slices = [1,2,3,4,5,6]
输出：10
解释：选择大小为 4 的披萨，Alice 和 Bob 分别挑选大小为 3 和 5 的披萨。然后你选择大小为 6 的披萨，Alice 和 Bob 分别挑选大小为 2 和 1 的披萨。你获得的披萨总大小为 4 + 6 = 10 。

示例 2：

1
2
3

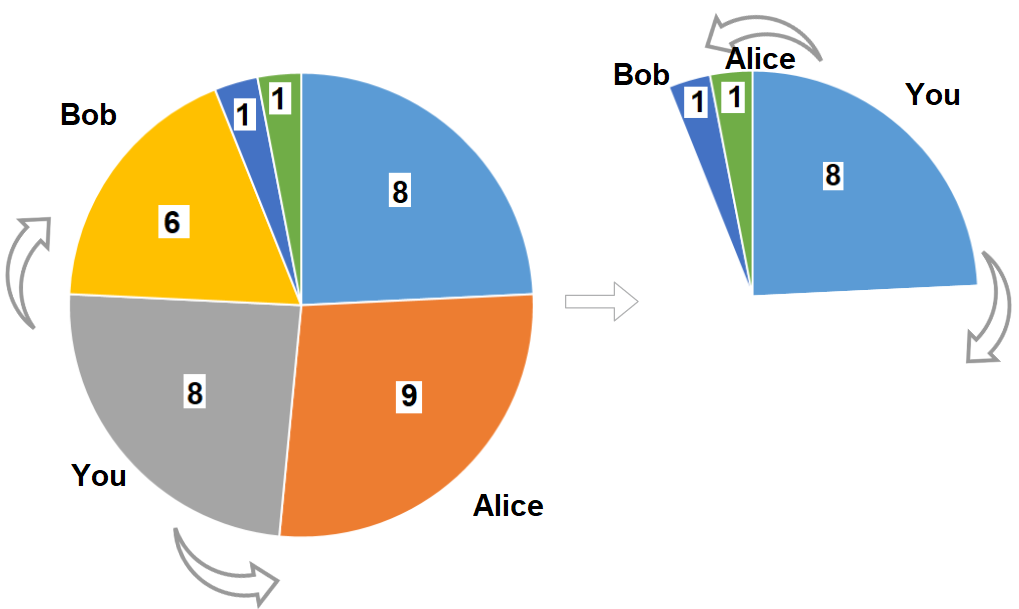
输入：slices = [8,9,8,6,1,1]
输出：16
解释：两轮都选大小为 8 的披萨。如果你选择大小为 9 的披萨，你的朋友们就会选择大小为 8 的披萨，这种情况下你的总和不是最大的。

提示：

1 <= slices.length <= 500
slices.length % 3 == 0
1 <= slices[i] <= 1000

问题转换+动态规划

问题转换为在3n个披萨中选择n个不相邻的披萨（注意首尾）

动态规划，首尾披萨不能同时选择，所以把数组首尾分别去除

得到两个数组slices[:-1]和slices[1:]，分别进行动态规划，最后取两个动态规划结果的大值

在前i个披萨中选j个

考虑是否选择第i个

dp[i][j] = max(dp[i-1][j], dp[i-2][j-1] + slices[i-1])

class Solution {
    public int maxSizeSlices(int[] slices) {
        int m = slices.length, n = m / 3, dp[][] = new int[m][n+1];
        for (int i = 1; i < m; i++) {  // slices[:-1]
            for (int j = 1; j <= n; j++) {
                dp[i][j] = Math.max(dp[i-1][j], (i-2 >= 0 ? dp[i-2][j-1] : 0) + slices[i-1]);
            }
        }
        int dp2[][] = new int[m][n+1];
        for (int i = 1; i < m; i++) {  // slices[1:]
            for (int j = 1; j <= n; j++) {
                dp2[i][j] = Math.max(dp2[i-1][j], (i-2 >= 0 ? dp2[i-2][j-1] : 0) + slices[i]);
            }
        }
        return Math.max(dp[m-1][n], dp2[m-1][n]);
    }
}

切披萨的方案数（2127）

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： 'A' （表示苹果）和 '.' （表示空白格子）。你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含至少一个苹果的切披萨方案数。由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

示例 1：

1
2
3

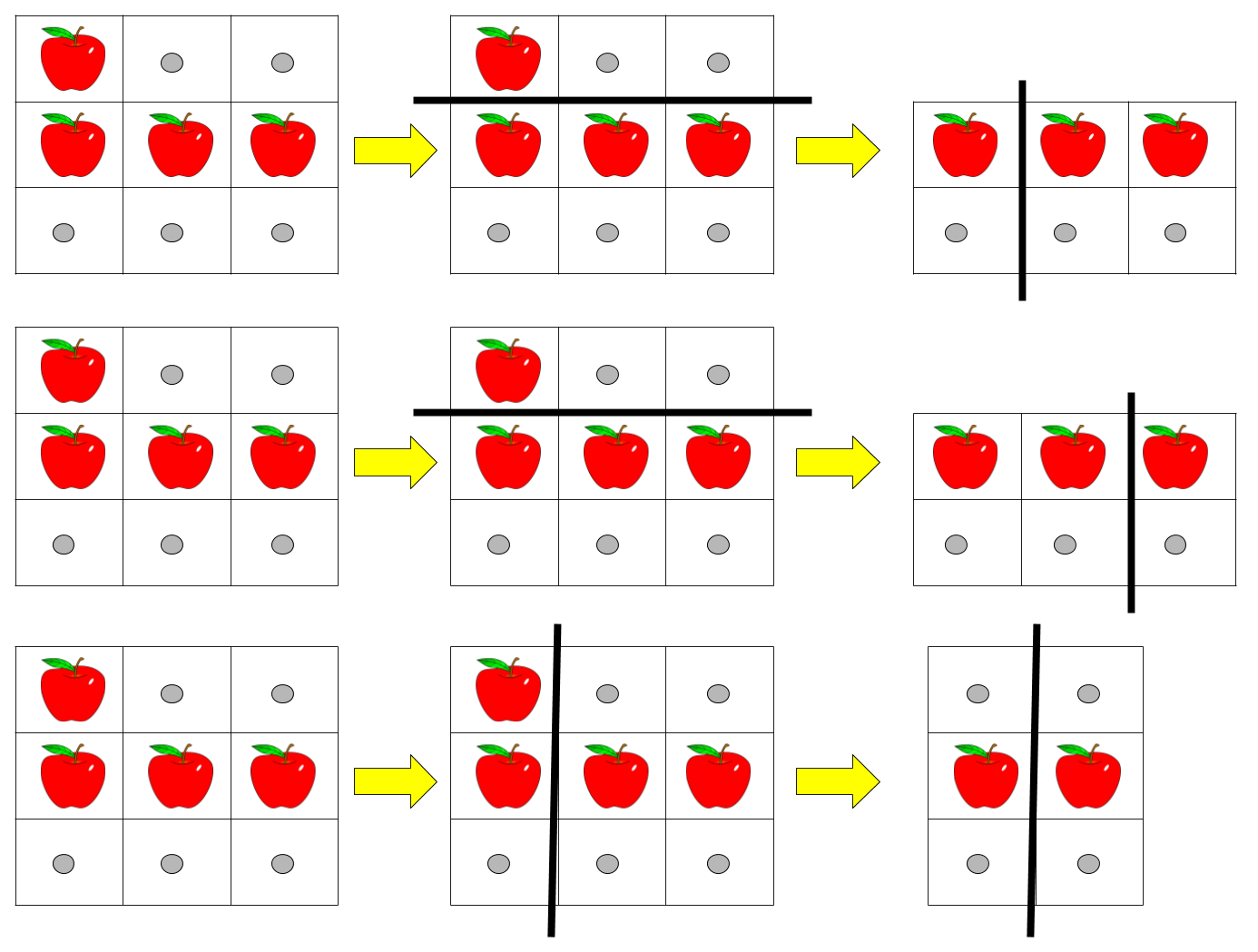
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。

示例 2：

1 2	输入：pizza = ["A..","AA.","..."], k = 3 输出：1

示例 3：

1 2	输入：pizza = ["A..","A..","..."], k = 1 输出：1

提示：

1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

bfs找所有矩形苹果数量+记忆化搜索

import java.util.Deque;
import java.util.LinkedList;

class Solution {
    int MOD = (int)1e9+7;
    public int ways(String[] pizza, int k) {
        int m = pizza.length, n = pizza[0].length();
        char [][]cs = new char[m][];
        for (int i = 0; i < m; i++) {
            cs[i] = pizza[i].toCharArray();
        }
        boolean haveApple[][][][] = new boolean[m+1][m+1][n+1][n+1];  // up down left right
        Deque<int[]> queue = new LinkedList<>();
        // 通过bfs找到所有包含苹果的矩形空间（用up和down两条row以及left和right两条col包围）
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (cs[i][j] == 'A') {
                    queue.offer(new int[]{i, i+1, j, j+1});
                    haveApple[i][i+1][j][j+1] = true;
                }
            }
        }
        while (!queue.isEmpty()) {
            int sz = queue.size();
            for (int i = 0; i < sz; i++) {
                int poll[] = queue.poll();
                int up = poll[0], down = poll[1], left = poll[2], right = poll[3];
                // System.out.println(up + " " + left + " " + down + " " + right);
                int newUp = up-1, newLeft = left-1, newDown = down+1, newRight = right+1;
                if (newUp >= 0 && !haveApple[newUp][down][left][right]) {
                    haveApple[newUp][down][left][right] = true;
                    queue.offer(new int[]{newUp, down, left, right});
                }
                if (newDown <= m && !haveApple[up][newDown][left][right]) {
                    haveApple[up][newDown][left][right] = true;
                    queue.offer(new int[]{up, newDown, left, right});
                }
                if (newLeft >= 0 && !haveApple[up][down][newLeft][right]) {
                    haveApple[up][down][newLeft][right] = true;
                    queue.offer(new int[]{up, down, newLeft, right});
                }
                if (newRight <= n && !haveApple[up][down][left][newRight]) {
                    haveApple[up][down][left][newRight] = true;
                    queue.offer(new int[]{up, down, left, newRight});
                }
            }
        }
        return dfs(cs, haveApple, 0, 0, 1, k, new int[(m+1)][(n+1)][k+1]);
    }
    // 通过dfs查找所有的切割方案
    public int dfs(char[][] cs, boolean[][][][] haveApple, int up, int left, int cur, int target, int[][][] cache) {
        int m = cs.length, n = cs[0].length, res = 0;
        // System.out.println("up: " + up + " left: " + left);
        if (cache[up][left][cur] != 0) return cache[up][left][cur];
        if (cur == target) {
            return haveApple[up][m][left][n] ? 1 : 0;
        }
        for (int i = up+1; i < m; i++) {  // 横切
            // 上半部分 and 下半部分
            if (haveApple[up][i][left][n] && haveApple[i][m][left][n]) {
                res = (res + dfs(cs, haveApple, i, left, cur+1, target, cache)) % MOD;
            }
        }
        for (int j = left+1; j < n; j++) {  // 竖切
            // 左半部分 and 右半部分
            if (haveApple[up][m][left][j] && haveApple[up][m][j][n]) {
                res = (res + dfs(cs, haveApple, up, j, cur+1, target, cache)) % MOD;
            }
        }
        cache[up][left][cur] = res;
        return res;
    }
}

容斥原理获取坐标右下矩形的苹果数量+动态规划

其实，不需要通过bfs获取所有矩形的苹果数量，只需要获取坐标右下方矩形中的苹果数量，分割时通过相减便知道分割两边的矩形苹果数量

获取坐标右下矩形的苹果数量，只需要从右下角往左上角遍历即可，并通过容斥原理计算:

apple[i][j] = cs[i][j] + apple[i+1][j] + apple[i][j+1] - apple[i+1][j+1]

从1到k块披萨进行动态规划

import java.util.Deque;
import java.util.LinkedList;

class Solution {
    int MOD = (int)1e9+7;
    public int ways(String[] pizza, int k) {
        int m = pizza.length, n = pizza[0].length();
        char cs[][] = new char[m][];
        for (int i = 0; i < m; i++) {
            cs[i] = pizza[i].toCharArray();
        }
        int apple[][] = new int[m+1][n+1];
        int dp[][][] = new int[k][m][n];
        // 通过容斥原理计算坐标右下矩形的苹果数量
        for (int i = m-1; i >= 0; i--) {
            for (int j = n-1; j >= 0; j--) {
                apple[i][j] = (cs[i][j] == 'A' ? 1 : 0) + apple[i+1][j] + apple[i][j+1]  - apple[i+1][j+1];
                dp[0][i][j] = apple[i][j] > 0 ? 1 : 0;
            }
        }
        for (int t = 1; t < k; t++) {
            for (int i = m-1; i >= 0; i--) {  // 这里i从0到m-1也可以，和顺序没关系
                for (int j = n-1; j >= 0; j--) {
                    // 横切
                    for (int x = i+1; x < m; x++) {
                        if (apple[x][j] > 0 && apple[i][j]-apple[x][j] > 0) dp[t][i][j] = (dp[t][i][j] + dp[t-1][x][j]) % MOD;
                    }
                    // 竖切
                    for (int y = j+1; y < n; y++) {
                        if (apple[i][y] > 0 && apple[i][j]-apple[i][y] > 0) dp[t][i][j] = (dp[t][i][j] + dp[t-1][i][y]) % MOD;
                    }
                }
            }
        }
        return dp[k-1][0][0];
    }
}

使数组和小于等于 x 的最少时间（2979）

给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒，对于所有下标 0 <= i < nums1.length ，nums1[i] 的值都增加 nums2[i] 。操作 完成后 ，你可以进行如下操作：

选择任一满足 0 <= i < nums1.length 的下标 i ，并使 nums1[i] = 0 。

同时给你一个整数 x 。

请你返回使 nums1 中所有元素之和 小于等于 x 所需要的最少时间，如果无法实现，那么返回 -1 。

示例 1：

输入：nums1 = [1,2,3], nums2 = [1,2,3], x = 4
输出：3
解释：
第 1 秒，我们对 i = 0 进行操作，得到 nums1 = [0,2+2,3+3] = [0,4,6] 。
第 2 秒，我们对 i = 1 进行操作，得到 nums1 = [0+1,0,6+3] = [1,0,9] 。
第 3 秒，我们对 i = 2 进行操作，得到 nums1 = [1+1,0+2,0] = [2,2,0] 。
现在 nums1 的和为 4 。不存在更少次数的操作，所以我们返回 3 。

示例 2：

1
2
3

输入：nums1 = [1,2,3], nums2 = [3,3,3], x = 4
输出：-1
解释：不管如何操作，nums1 的和总是会超过 x 。

提示：

1 <= nums1.length <= 10^3
1 <= nums1[i] <= 10^3
0 <= nums2[i] <= 10^3
nums1.length == nums2.length
0 <= x <= 10^6

动态规划找极值

假设第j次操作，选择的数是i
那么增加的量为sum(nums2)，减少的量为nums1[i] + t*nums2[i]
增加的量是固定值，减少量是变化的，我们需要最大化减少量
假设我们已经确定要对第 a1, a2, ..., at 个元素进行操作，那么我们可以确定的“收益”就是 nums1[a1] + nums1[a2] + ... + nums1[at]。接下来要确定的就是操作元素的顺序，使得最终的“收益”最大。我们没有确定的收益就是 x * nums2[i]，显然应该把更大的 x 分给更大的 nums2[i]。也就是说，一定是按 nums2[i] 从小到大的顺序操作元素。（nums2是有优先级的）
用 dp[i][j] 表示在前 i 个元素中操作了 j 次的最大减少量
dp[n][j] 则表示操作不同次数(j次)的最大减少量

import java.util.List;
class Solution {
    public int minimumTime(List<Integer> nums1, List<Integer> nums2, int x) {       
        int nums[][] = new int[nums1.size()][], n = nums.length, sum1 = 0, sum2 = 0, dp[][] = new int[n+1][n+1];
        for (int i = 0; i < n; i++) {
            nums[i] = new int[]{nums1.get(i), nums2.get(i)};
            sum1 += nums1.get(i);
            sum2 += nums2.get(i);
        }
        Arrays.sort(nums, (a,b)->a[1]-b[1]);
        /**
         *   j(操作j次) 
         * i 1 0 0
         *   1 1 0  ↓
         *   1 1 1
         */
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-1] + nums[i-1][0] + j*nums[i-1][1]);
            }
        }
        for (int j = 0; j <= n; j++) {
            if (sum1 + j*sum2 - dp[n][j] <= x) return j;
        }                        
        return -1;
    }
}

卖木头块（2363）

给你两个整数 m 和 n ，分别表示一块矩形木块的高和宽。同时给你一个二维整数数组 prices ，其中 prices[i] = [hi, wi, pricei] 表示你可以以 pricei 元的价格卖一块高为 hi 宽为 wi 的矩形木块。

每一次操作中，你必须按下述方式之一执行切割操作，以得到两块更小的矩形木块：

沿垂直方向按高度完全切割木块，或
沿水平方向按宽度完全切割木块

在将一块木块切成若干小木块后，你可以根据 prices 卖木块。你可以卖多块同样尺寸的木块。你不需要将所有小木块都卖出去。你不能旋转切好后木块的高和宽。

请你返回切割一块大小为 m x n 的木块后，能得到的最多钱数。

注意你可以切割木块任意次。

示例 1：

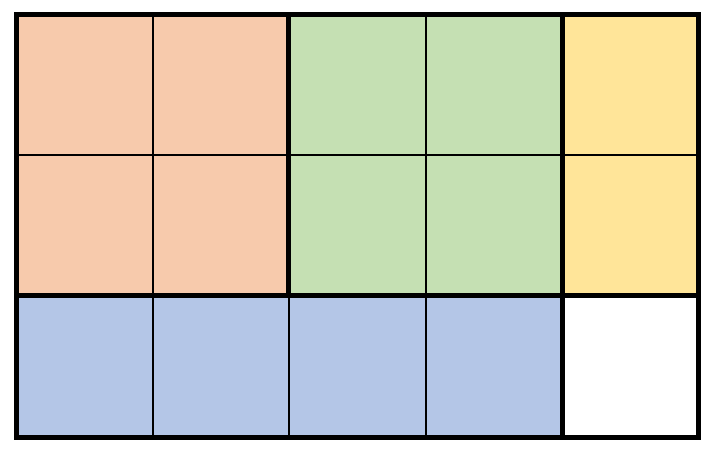
输入：m = 3, n = 5, prices = [[1,4,2],[2,2,7],[2,1,3]]
输出：19
解释：上图展示了一个可行的方案。包括：
- 2 块 2 x 2 的小木块，售出 2 * 7 = 14 元。
- 1 块 2 x 1 的小木块，售出 1 * 3 = 3 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 14 + 3 + 2 = 19 元。
19 元是最多能得到的钱数。

示例 2：

输入：m = 4, n = 6, prices = [[3,2,10],[1,4,2],[4,1,3]]
输出：32
解释：上图展示了一个可行的方案。包括：
- 3 块 3 x 2 的小木块，售出 3 * 10 = 30 元。
- 1 块 1 x 4 的小木块，售出 1 * 2 = 2 元。
总共售出 30 + 2 = 32 元。
32 元是最多能得到的钱数。
注意我们不能旋转 1 x 4 的木块来得到 4 x 1 的木块。

提示：

1 <= m, n <= 200
1 <= prices.length <= 2 * 10^4
prices[i].length == 3
1 <= hi <= m
1 <= wi <= n
1 <= pricei <= 10^6
所有 (hi, wi) 互不相同 。

Java

/**
    定义 f[i][j] 表示切割一块高 i 宽 j 的木块，能得到的最多钱数。
 */
class Solution {
    public long sellingWood(int m, int n, int[][] prices) {
        long f[][] = new long[m+1][n+1];
        for (int price[] : prices) {
            f[price[0]][price[1]] = price[2];
        }
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                for (int k = 1; k <= j/2; k++) f[i][j] = Math.max(f[i][j], f[i][k] + f[i][j-k]);
                for (int k = 1; k <= i/2; k++) f[i][j] = Math.max(f[i][j], f[k][j] + f[i-k][j]);
            }
        }
        return f[m][n];
    }
}

algorithm-dp-misc

更多

石子游戏 V（2087

记忆化搜索(1750ms)

动态规划(280ms)

英雄的力量（2060）

找规律动态规划

常规思路动态规划+前缀和

3n 块披萨（2410）

问题转换+动态规划

切披萨的方案数（2127）

bfs找所有矩形苹果数量+记忆化搜索

容斥原理获取坐标右下矩形的苹果数量+动态规划

使数组和小于等于 x 的最少时间（2979）

动态规划找极值

卖木头块（2363）

Java